Introduction¶

This guide provides information for developers who want to use the Couchbase Java SDK to build applications that use Couchbase Server.

Getting Started¶

Now that you have installed Couchbase and have probably created a cluster of Couchbase servers, it is time to install the client libraries, couchbase-client and spymemcached, and start storing data into the clusters.

Here’s a quick outline of what you’ll learn in this chapter:

1. Download the Java Couchbase Client Libraries, couchbase-client and spymemcached.

2. Create an Eclipse or NetBeans project and set up the Couchbase Client Libraries as referenced libraries. You’ll need to include these libraries at compile time, which should propagate to run time.

3. Write a simple program to demonstrate connecting to Couchbase and saving some data.

4. Explore some of the API methods that will take you further than the simple program.

This section assumes you have downloaded and set up a compatible version of Couchbase Server and have at least one instance of Couchbase Server and one data bucket established. If you need to set up these items, you can do with the Couchbase Administrative Console, or Couchbase Command-Line Interface (CLI), or the Couchbase REST API. For information and instructions, see:

• Using the Couchbase Web Console, for information on using the Couchbase Administrative Console,

• Couchbase CLI, for the command line interface,

• Couchbase REST API, for creating and managing Couchbase resources.

The TCP/IP port allocation on Windows by default includes a restricted number of ports available for client communication. For more information on this issue, including information on how to adjust the configuration and increase the available ports, see MSDN: Avoiding TCP/IP Port Exhaustion.

After you have your Couchbase Server set up and you have installed SDK, you can compile and run the following basic program.

Downloading the Couchbase Client Libraries¶

Download the Client libraries and its dependencies and make sure they are available in the classpath. Please refer to for installation of the client JAR files and the dependencies and for running them. You can download them directly from the Java client libraries for Couchbase.

These are Java Archive ( .jar ) files that you can use with your Java environment.

Hello Couchbase¶

You might be curious what the simplest Java program to talk to Couchbase might look like, and how you might compile and run it using just the Java command line tools. Follow along if you like and look at Listing 1.

Listing 1: Main.java

import java.net.URI;
import java.util.LinkedList;
import java.util.List;
import java.util.concurrent.TimeUnit;

import com.couchbase.client.CouchbaseClient;
import net.spy.memcached.internal.GetFuture;
import net.spy.memcached.internal.OperationFuture;

public class Main {
  public static final int EXP_TIME = 10;
  public static final String KEY = "spoon";
  public static final String VALUE = "Hello World!";

  public static void main(String args[]) {
    // Set the URIs and get a client
    List<URI> uris = new LinkedList<URI>();

    Boolean do_delete = false;

    // Connect to localhost or to the appropriate URI
    uris.add(URI.create("http://127.0.0.1:8091/pools"));

    CouchbaseClient client = null;
    try {
      client = new CouchbaseClient(uris, "default", "");
    } catch (Exception e) {
      System.err.println("Error connecting to Couchbase: "
        + e.getMessage());
      System.exit(0);
    }
    // Do a synchrononous get
    Object getObject = client.get(KEY);
    // Do an asynchronous set
    OperationFuture<Boolean> setOp = client.set(KEY, EXP_TIME, VALUE);
    // Do an asynchronous get
    GetFuture getOp = client.asyncGet(KEY);
    // Do an asynchronous delete
    OperationFuture<Boolean> delOp = null;
    if (do_delete) {
      delOp = client.delete(KEY);
    }
    // Shutdown the client
    client.shutdown(3, TimeUnit.SECONDS);
    // Now we want to see what happened with our data
    // Check to see if our set succeeded
    try {
      if (setOp.get().booleanValue()) {
        System.out.println("Set Succeeded");
      } else {
        System.err.println("Set failed: "
            + setOp.getStatus().getMessage());
      }
    } catch (Exception e) {
      System.err.println("Exception while doing set: "
          + e.getMessage());
    }
    // Print the value from synchronous get
    if (getObject != null) {
      System.out.println("Synchronous Get Suceeded: "
          + (String) getObject);
    } else {
      System.err.println("Synchronous Get failed");
    }
    // Check to see if ayncGet succeeded
    try {
      if ((getObject = getOp.get()) != null) {
        System.out.println("Asynchronous Get Succeeded: "
            + getObject);
      } else {
        System.err.println("Asynchronous Get failed: "
            + getOp.getStatus().getMessage());
      }
    } catch (Exception e) {
      System.err.println("Exception while doing Aynchronous Get: "
          + e.getMessage());
    }
    // Check to see if our delete succeeded
    if (do_delete) {
      try {
        if (delOp.get().booleanValue()) {
          System.out.println("Delete Succeeded");
        } else {
          System.err.println("Delete failed: " +
              delOp.getStatus().getMessage());
        }
      } catch (Exception e) {
        System.err.println("Exception while doing delete: "
            + e.getMessage());
      }
    }
  }
}

1. Enter the code in listing 1 into a file named Main.java

2. Download the couchbase-client and spymemcached client libraries for Java. You will also need the dependent JAR files as well, as listed in the execution instructions below. One simple way to obtain the JAR and all dependencies is through the Maven repository.

3. Type the following commands:

   shell> javac -cp couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar \
          Main.java
    shell> java -cp .:couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar:\
    jettison-1.1.jar:netty-3.2.0.Final.jar:commons-codec-1.5.jar Main
   

Of course, substitute your own Couchbase server IP address. If you are on Linux or MacOS replace the semi-colon in the second command-line with a colon. The program will produce the following output:

2012-01-16 15:06:29.265 INFO com.couchbase.client.CouchbaseConnection:  Added {QA sa=/127.0.0.1:11210, #Rops=0, #Wops=0, #iq=0, topRop=null, topWop=null, toWrite=0, interested=0} to connect queue
2012-01-16 15:06:29.277 INFO com.couchbase.client.CouchbaseConnection:  Connection state changed for sun.nio.ch.SelectionKeyImpl@1d3c468a
2012-01-16 15:06:29.420 INFO com.couchbase.client.CouchbaseConnection:  Shut down Couchbase client
Synchronous Get failed
Set Succeeded
Asynchronous Get Succeeded: Hello World!

Much of this output is logging statements produced by the client library, to inform you of what’s going on inside the client library to help you diagnose issues. It says that a connection to Couchbase was added and that the connection state changed. Then the code shows that the key spoon did not exist in Couchbase which is why the Synchronous Get failed.

Running the program again, within 10 seconds will produce the following output:

2012-01-16 15:37:12.242 INFO com.couchbase.client.CouchbaseConnection:  Added {QA sa=/127.0.0.1:11210, #Rops=0, #Wops=0, #iq=0, topRop=null, topWop=null, toWrite=0, interested=0} to connect queue
2012-01-16 15:37:12.253 INFO com.couchbase.client.CouchbaseConnection:  Connection state changed for sun.nio.ch.SelectionKeyImpl@7f2ad19e
2012-01-16 15:37:12.439 INFO com.couchbase.client.CouchbaseConnection:  Shut down Couchbase client
Synchronous Get Succeeded: Hello World!
Set Succeeded
Asynchronous Get Succeeded: Hello World!

Again you see the log statements, followed by the indication that this time, the key spoon was found in Couchbase with the value “Hello World!” as evidenced in the Synchronous Get succeeding. Run the same piece of code after 10 seconds or set the do_delete flag to true and notice the changed behavior of the program. It is possible to get the precise message from the server in the case of a failure by calling the getOp.getStatus().getMessage() method on the Operation.

Congratulations, you’ve taken your first small step into a much larger world.

Couchbase API Overview¶

The Couchbase client library has many API methods that you can use to implement your distributed memory magic. The client library methods below are grouped into categories so that you’ll have a quick reference you can refer to later.

decr	Decrement a key and return the value.
get	Gets a particular value from the cache.
getBulk	Gets many values at the same time.
gets	Gets a particular value with Check And Set support.
incr	Increment the value of a key.

cas | Perform a Check And Set operation. ——|———————————–

add	Adds an object to the cache if it does not exist already.
delete	Deletes a value from the cache.
flush	Clears the cache on all servers.
append	Append to an existing value in the cache.
asyncCAS	Check and set values of particular keys.
asyncDecr	Decrement a value.
asyncGet	Get a particular value.
asyncGetBulk	Get many values at the same time.
asyncGets	Get a value with CAS support.
asyncIncr	Increment a value.

addObserver	Adds an observer to watch the connection status.
getAvailableServers	Returns a list of available servers.
getNodeLocator	Returns a read only instance of the node locator.
getStats	Returns connection statistics.
getTranscoder	Returns the default transcoder instance.
getUnavailableServers	Returns a list of the servers that are not available.
getVersions	Returns the versions of all connected servers.

A More Substantial Program¶

Please download the Sample Code if you’re interested in making a more substantial program that you can run. The program will create a user specified number of threads, that each try to create (or read from Couchbase) 100 random numbers. The code creates a CouchbaseClient object instance for each thread, and then proceeds to perform a gets() operation looking for specific keys. The gets() operation will return null if the key has not been set. In this case the thread will create the value itself and set it into Couchbase and it will incur a 100 millisecond penalty for doing so. This simulates an expensive database operation. You can find the full source code for the small application attached to the end of this article.

Let’s discuss a few parts of the program, so you can understand the fundamentals of connecting to Couchbase servers, testing for the existence of particular key-value pairs, and setting a value to a key. These few operations will give you more of an idea of how to begin.

Listing 2. Connecting to a set of Couchbase servers:

URI server = new URI(addresses);

    ArrayList<URI> serverList = new ArrayList<URI>();

    serverList.add(server);
    CouchbaseClient client = new CouchbaseClient(
        serverList, "default", "");

You can see, from these lines that you’ll need to obtain an instance of a CouchbaseClient. There are numerous ways to construct one, but a constructor that is quite useful involved the ArrayList of URIs.

http://host-or-ip:port/pools

The port you will be connecting to will be the port 8091 which is effectively a proxy that knows about all of the other servers in the cluster and will provide quick protocol access. So in the case of this cluster, providing an addresses string as follows, worked very well:

String addresses = "10.0.0.33:8091/pools"

Listing 3 is an abridged excerpt that shows the creation of an IntegerTranscoder, which is a useful class for converting objects in Couchbase back to integers when needed. This is for convenience and reduces type casting. You can then see that a the gets() method is called. This returns a CASValue of type integer which is useful for checking and setting a value. If the value is null it means that Couchbase hasn’t been given a value for this key. The code then sets a value. Otherwise, we can get its value and do something with it.

Listing 3. Check And Set operations

IntegerTranscoder intTranscoder = new IntegerTranscoder();

    CASValue<Integer> value = client.gets(key,
        intTranscoder);

    if (value == null) {
        // The value doesn't exist in Couchbase
        client.set(key, 15, rand.nextInt(), intTranscoder);

        // Simulate the value taking time to create.
        Thread.sleep(100);

        created++;

    } else {

        int v = value.getValue();

    }

Setting values in Couchbase are done asynchronously, and the application does not have to wait for these to be completed. Sometimes, though, you may want to ensure that Couchbase has been sent some values, and you can do this by calling client.waitForQueues() and giving it a timeout for waiting for this to occur, as shown in Listing 4.

Listing 4. Waiting for the data to be set into Couchbase.

client.waitForQueues(1, TimeUnit.MINUTES);

How to Build and Run the Sample Application¶

Download the entire Java Getting Started Source code and follow along with the steps.

You can compile and run the program using the following steps.

shell> javac -cp couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar \
    GettingStarted.java
shell> java -cp .:couchbase-client-1.0.0.jar:\
spymemcached-2.8.0.jar:jettison-1.1.jar:netty-3.2.0.Final.jar:\
commons-codec-1.5.jar GettingStarted http://192.168.3.104:8091/pools 10

Running this program generates the following output the first time:

Client-2 took 37.2500 ms per key. Created 35. Retrieved 65 from cache.
Client-3 took 37.7800 ms per key. Created 35. Retrieved 65 from cache.
Client-4 took 37.7100 ms per key. Created 35. Retrieved 65 from cache.
Client-0 took 37.8300 ms per key. Created 35. Retrieved 65 from cache.
Client-1 took 37.8400 ms per key. Created 35. Retrieved 65 from cache.

Running the program a second time before 15 seconds elapses, produces this output instead:

Client-1 took 4.6700 ms per key. Created 0. Retrieved 100 from cache.
Client-3 took 4.6000 ms per key. Created 0. Retrieved 100 from cache.
Client-4 took 4.7500 ms per key. Created 0. Retrieved 100 from cache.
Client-2 took 4.7900 ms per key. Created 0. Retrieved 100 from cache.
Client-0 took 4.8400 ms per key. Created 0. Retrieved 100 from cache.

There are a few things that are interesting about the output. In the first scenario, the five threads collaborate to produce the sequence of random numbers such that the average time per key is significantly less than 100ms. Each thread is creating 35 numbers, but reading 65 from the cache.

In the second run, because the 15 second timeout has not elapsed yet, all of the random numbers were retrieved from the cache by all of the threads. Notice that reading these values from Couchbase only takes a few milliseconds.

The complete source code for this is below. You would run this with the command line arguments like below after ensuring that the client libraries are included in the classpath.

shell> javac -cp couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar \
    GettingStarted.java
shell> java -cp .:couchbase-client-1.0.0.jar:\
spymemcached-2.8.0.jar:jettison-1.1.jar:netty-3.2.0.Final.jar:\
commons-codec-1.5.jar GettingStarted http://192.168.3.104:8091/pools 10

import java.util.Random;
import java.util.concurrent.CountDownLatch;
import java.util.concurrent.TimeUnit;
import java.util.ArrayList;

import java.net.URI;

import com.couchbase.client.CouchbaseClient;

import net.spy.memcached.CASValue;
import net.spy.memcached.transcoders.IntegerTranscoder;

/**
 * Sets up a number of threads each cooperating to generate a set of random
 * numbers and illustrates the time savings that can be achieved by using
 * Couchbase.
 */
public class GettingStarted {

    static final int numIntegers = 100;
    static String addresses;
    static CountDownLatch countdown;

    /**
     * @param args
     */
    public static void main(String[] args) {

        if (args.length < 2) {
            System.err.println("usage: addresses numthreads");
            System.exit(1);
        }

        addresses = args[0];

        int numThreads = Integer.parseInt(args[1]);

        countdown = new CountDownLatch(numThreads);

        for (int i = 0; i < numThreads; i++) {
            Thread t = new Thread(new ClientThread(String.format(
                    "Client-%d", i)));
            t.setName("Client Thread " + i);
            t.start();
        }

        try {
            countdown.await();
        } catch (InterruptedException e) {
        }

        System.exit(0);
    }

    private static class ClientThread implements Runnable {

        private String name;

        public ClientThread(String name) {
            this.name = name;
        }

        @Override
        public void run() {

            try {
                URI server = new URI(addresses);

                ArrayList<URI> serverList = new ArrayList<URI>();

                serverList.add(server);

                CouchbaseClient client = new CouchbaseClient(
                        serverList, "default", "");
                IntegerTranscoder intTranscoder = new IntegerTranscoder();

                // Not really random, all threads
                // will have the same seed and sequence of
                // numbers.
                Random rand = new Random(1);

                long startTime = System.currentTimeMillis();

                int created = 0;
                int cached = 0;

                for (int i = 0; i < numIntegers; i++) {
                    String key = String.format("Value-%d", i);

                    CASValue<Integer> value = client.gets(key,
                            intTranscoder);

                    if (value == null) {
                        // The value doesn't exist in Membase
                        client.set(key, 15, rand.nextInt(), intTranscoder);

                        // Simulate the value taking time to create.
                        Thread.sleep(100);

                        created++;

                    } else {

                        // The value does exist, another thread
                        // created it already so this thread doesn't
                        // have to.
                        int v = value.getValue();

                        // Check that the value is what we
                        // expect it to be.
                        if (v != rand.nextInt()) {
                            System.err.println("No match.");
                        }
                        cached++;
                    }

                    client.waitForQueues(1, TimeUnit.MINUTES);
                }

                System.err.println(String.format(
                        "%s took %.4f ms per key. Created %d."
                                + " Retrieved %d from cache.", name,
                        (System.currentTimeMillis() - startTime)
                                / (double)numIntegers, created, cached));

            } catch (Throwable ex) {
                ex.printStackTrace();
            }

            countdown.countDown();
        }
    }
}

Conclusion¶

You now know how to obtain the Couchbase Java client libraries, and write small Java programs to connect with your Couchbase cluster and interact with it. Congratulations, you will be able to save your servers from burning down, and impress your users with the blazing fast response that your application will be able to achieve.

Tutorial¶

In order to follow this tutorial the following need to be installed and functional.

• Java SE 6 (or higher) installed

• Couchbase server installed and running

• Client libraries installed and available in the classpath. Please refer to for installation of the client JAR files and the dependencies and for running them.

Installation¶

1. Download the Java client libraries for Couchbase

2. Download the entire Java Tutorial Source code and follow along with the steps.

Building a Chat Room Application¶

You will be writing a distributed chat room application, where a nearly unlimited number of people could potentially be talking at the same time. The previous statements made by other users will be remembered in memory for a certain period of time, after which they will be forgotten. When a user first connects to the server they will be sent the entire transcript of messages that have not timed out on the server, after which they will be able to participate anonymously in the ongoing conversation. At any point in the conversation, they may quit, by typing the word ‘/quit’. Implementing these requirements will demonstrate a number of important API methods of the spymemcached driver talking to a Couchbase server, which is providing the distributed storage capabilities.

Let’s get started.

Connecting with the Server¶

The driver library contains a number of different ways to connect to a Couchbase server. First, I will begin with a discussion of these methods and then we will use one of those methods to make the chat room client application connect with your Couchbase installation.

There are more than one way of connecting with one or more Couchbase servers from the driver:

1. A direct connection can be made by creating an instance of the CouchbaseClient object and passing in one or more addresses. For example:

   URI server = new URI(addresses);
                    ArrayList<URI> serverList = new ArrayList<URI>();
                    serverList.add(server);
                    CouchbaseClient client = new CouchbaseClient(
                            serverList, "default", "");
   

   It’s recommended to provide more than one server address of all the servers participating in the Couchbase cluster since the client can recover easily if the original server goes down.

2. Use the connection factory CouchbaseConnectionFactory constructors to establish a connection with your server:

   URI base = new URI(String.format(
             "http://%s:8091/pools", serverAddress));
        ArrayList<URI> serverList = new ArrayList<URI>();
        serverList.add(base);
        CouchbaseConnectionFactory cf = new CouchbaseConnectionFactory(serverList,
           "default", "");
   

3. Create a connection that is authenticated using SASL by using a CouchbaseConnectionFactory. Merely specifying the authenticated bucket will establish an authenticated connection. In the case of Couchbase, the username and password you use here are based on the buckets you have defined on the server. The username is the bucket name, and the password is the password used when creating the bucket. I will talk more about this later, in the meantime here is the code you will need to authenticate and start using a bucket with SASL authentication.

   CouchbaseConnectionFactory cf = new CouchbaseConnectionFactory(baseURIs,
           "rags", "password");
        client = new CouchbaseClient((CouchbaseConnectionFactory) cf);
   

Let’s start making modifications to the tutorial Main.java class in order to make our first connection. Here we will be making an unauthenticated ASCII protocol connection to the server. After you have the tutorial code working, you can easily go back and change the connect() method to use authentication.

First you modify your main() method as follows:

public static void main(String[] args) {

    if (args.length != 1) {
        System.err.println("usage: serveraddress");
        System.exit(1);
    }

    String serverAddress = args[0];

    System.out.println(String.format("Connecting to %s",serverAddress));

     try {

             connect(serverAddress);
             client.shutdown(1, TimeUnit.MINUTES);

    } catch (IOException ex) {
            ex.printStackTrace();
    }

}

Next, add the connect() method.

private void connect(String serverAddress) throws Exception {

        URI base = new URI(String.format("http://%s:8091/pools",serverAddress));
        List<URI> baseURIs = new ArrayList<URI>();
        baseURIs.add(base);
        CouchbaseConnectionFactory cf = new
                CouchbaseConnectionFactory(baseURIs, "default", "");

        client = new CouchbaseClient((CouchbaseConnectionFactory) cf);

You’ll recognize this constructor as a single server connection. What if you want to know more about the current connection state such as when the connection has been gained, or lost? You can add a connection observer by modifying the connect method and adding the following lines:

public void connectionLost(SocketAddress sa) {
                System.out.println("Connection lost to " + sa.toString());
            }

            public void connectionEstablished(SocketAddress sa,
                    int reconnectCount) {
                System.out.println("Connection established with "
                        + sa.toString());
                System.out.println("Reconnected count: " + reconnectCount);
            }
        });

    }

You’ve only connected with one server, what if it goes offline? This can easily be fixed by changing the first three lines of the connect method:

URI fallback = new URI(
            String.format("http://%s:8091/pools",fallbackAddress));
        baseURIs.add(fallback);

This class will even work with colon-delimited IPv6 addresses.

Finally, you need to create the static member variable to store the client instance at the top of the class:

private static CouchbaseClient client;

Now you can try compiling and running the application.

You can see that the driver outputs some logging statements indicating that it is making two connections. You can also see that the connection observer you added to the connect() method is being called with the addresses of the two servers as they are connected and the reconnection count is 1 indicating that the network is in good shape. It’s ready to get some work done.

Logging in the Chat Application¶

For the purpose of this tutorial, we will use the spymemcached logging framework. The Couchbase Java SDK is compatible with the framework. There are two other approaches to logging with the Java SDK either by setting JDK properties, or by logging from an application. For more information, see Configuring Logging

To provide logging via spymemcached:

System.setProperty("net.spy.log.LoggerImpl", "net.spy.memcached.compat.log.SunLogger");

or

System.setProperty("net.spy.log.LoggerImpl", "net.spy.memcached.compat.log.Log4JLogger");

The default logger simply logs everything to the standard error stream.

Shutting Down a Client Connection¶

The client application will remain running until the client.shutdown() or client.shutdown(long, TimeUnit) methods are called.

The shutdown() method shuts the application down immediately and any outstanding work will be stopped.

The shutdown(long, TimeUnit) method will actually wait until any outstanding queued work is completed before shutting down, but it will time out in the given period of time. This would be the preferred method of shutting down the client connection.

Increment and Decrement Operations¶

The API contains methods that are able to atomically increment a variable in the cache and decrement a variable. Effectively this means that these operations are safe for use by any client across the cluster at any time and there is some guarantee that these will be done in the right order. We will demonstrate these methods by tracking the total number of chat clients connected to the server.

Add the following lines to the Main method after the connect method:

try {
    connect(serverAddress);

    register();
    unregister();

    client.shutdown(1, TimeUnit.MINUTES);

} catch (IOException e) {
    e.printStackTrace();
}

Then add the following two methods to the end of the class:

private static boolean register() {

    userId = client.incr("UserId", 1, 1);
    System.out.println("You are user " + userId + ".");

    userCount = client.incr("UserCount", 1, 1);
    System.out.println("There are currently " + userCount + " connected.");

    return true;
}

private static void unregister() {

    client.decr("UserCount", 1);
    System.out.println("Unregistered.");

}

These two methods demonstrate the use of the incr and decr methods which increment and decrement a variable, respectively. The application you are building uses this to keep track of how many users are currently running the program. This particular overload of the incr method takes a default value which it will use if the key UserCount does not exist, and will return the current count. In this case the first user will be assigned user number 1. Finally, when the unregister method is called, the decr method will be called to subtract 1 from the UserCount value.

Finally, you must add the following static member variables to the top of the class:

private static long userId = 0;
private static long userCount = 0;

If you compile and run this program now, you will see the following output:

Reconnected count: -1
You are user 1.
Registration succeeded.
There are currently 1 connected.
Enter text, or /who to see user list, or /quit to exit.

Up to this point, the application is doing some very simple things, allowing a user to connect, and keeping track of how many users and currently connected. It’s time to start adding some data to the system, and providing some methods to interact between multiple clients.

Prepend and Append Operations¶

We have implemented a client application that tracks how many clients are connected at the moment. Let’s add the functionality to track the user numbers that are currently connected.

We’ll nominate a key to keep a list of all of the user numbers that are currently connected, and then when a user disconnects, remove their entry from the key. Right away, though, this presents a challenge. How can we guarantee that two users starting at exactly the same time don’t mess up the value by overwriting each other’s edits? Let’s find out.

The API contains a method called append. It takes a special value called a CAS, which stands for Check and Set, but where do we get this number? There is another method called gets which returns an object that can be asked for the CAS value we need to perform an append operation. Another interesting thing about the append method is that returns a Future<Boolean> which means it is an asynchronous method. You can use the value it returns to wait for an answer indicating whether the operation succeeded or failed. Asynchronous methods also allow the code to do other things without having to wait for the result. At a later point in the code, the result of the operation can be obtained by using the future variable.

You will be using the append method in this tutorial, but the prepend method functions in exactly the same way except that append adds a string to the end of a value in the cache, and prepend puts a string at the front of a value in the cache.

Both the append and prepend methods operate atomically, meaning they will perform the operation on a value in the cache and finish each operation before moving on to the next. You will not get interleaved appends and prepends. Of course, the absolute order of these operations is not guaranteed.

The lines that are in bold-face should be changed in the register method of the code.

private static String getUserNameToken() {
     return String.format("<User-%d>", userId);
}

private static boolean register() {

    userId = client.incr("UserId", 1, 1);
    System.out.println("You are user " + userId + ".");

    CASValue<Object> casValue = client.gets("CurrentUsers");

    if (casValue == null) {

        System.out.println("First user ever!");

        try {
            client.set("CurrentUsers", Integer.MAX_VALUE,
                    getUserNameToken()).get();
        } catch (InterruptedException e) {
            e.printStackTrace();
        } catch (ExecutionException e) {
            e.printStackTrace();
        }

    } else {

        Future<Boolean> appendDone = client.append(casValue.getCas(),
                "CurrentUsers", getUserNameToken());

        try {

            if (appendDone.get()) {
                System.out.println("Registration succeeded.");
            } else {
                System.out.println("Sorry registration failed.");
                return false;
            }

        } catch (InterruptedException e) {
            e.printStackTrace();
            return false;
        } catch (ExecutionException e) {
            e.printStackTrace();
            return false;
        }

    }

    userCount = client.incr("UserCount", 1, 1);
    System.out.println("There are currently " + userCount
            + " connected.");

    return true;
}

First you can see that the client.gets("CurrentUsers") method is called to get a casValue. If that value is null, it means that no one has ever connected, so that user is the first user. So we will simply set the value of CurrentUsers using the new getUserNameToken() method.

Otherwise, we will append our userid to the list of users. To do this, we need to call the append method with the CAS that is in the casValue by calling its getCas() method. The append method is also asynchronous and returns a Future<Boolean>. Calling the get() method on that future will return its value when its operation has been performed. The append operation can possibly fail, if for instance the size of the list of usernames exceeds the maximum size of a value in the cache. So we handle both cases. If it returns true, we tell the user that the registration was a success. Otherwise the registration failed, so we’ll tell the user this and return false to tell the main program that something went wrong.

You need to modify the main method as well, to handle the possibility of the register method returning false.

try {
     connect(serverAddress);

     if (register()) {
         unregister();
     }

     client.shutdown(1, TimeUnit.MINUTES);

} catch (IOException e) {
    e.printStackTrace();
}

Now, we need to implement the cleanup of the user list when a user leaves. We will be modifying the unregister method to be very careful to remove the current userId from the CurrentUsers list before finishing. This is a potentially dangerous operation for a distributed cache since two or more users may try to exit the application at the same time and may try to replace the user list overwriting the previous changes. We will use a trick that effectively forces a distributed critical section.

private static void unregister() {

    try {
        // Wait for add to succeed. It will only
        // succeed if the value is not in the cache.
        while (!client.add("lock:CurrentUsers", 10, "1").get()) {
            System.out.println("Waiting for the lock...");
            Thread.sleep(500);
        }

        try {
            String oldValue = (String)client.get("CurrentUsers");
            String userNameToken = getUserNameToken();
            String newValue = oldValue.replaceAll(userNameToken, "");
            client.set("CurrentUsers", Integer.MAX_VALUE, newValue);
        } finally {
            client.delete("lock:CurrentUsers");
        }

    } catch (InterruptedException e) {
        e.printStackTrace();
    } catch (ExecutionException e) {
        e.printStackTrace();
    }

    client.decr("UserCount", 1);
    System.out.println("Unregistered.");

}

Here we use the fact that the client.add() method will succeed if and only if a value does not exist for the given key to provide a way for only one application to be able to edit the CurrentUsers at a time. We will call this lock:CurrentUsers and it will expire in ten seconds. If we are not able to add, the code will sleep for 500 milliseconds and try again.

The expiry time as defined in the protocol is documented as follows in the JavaDocs for the API:

The actual value sent may either be Unix time (number of seconds since January 1, 1970, as a 32-bit value), or a number of seconds starting from current time. In the latter case, this number of seconds may not exceed 60*60*24*30 (number of seconds in 30 days); if the number sent by a client is larger than that, the server will consider it to be real Unix time value rather than an offset from current time.

Once the add succeeds, a try/finally block is entered that actually gets the value of CurrentUsers and edits it, replacing the current user token with the empty string. Then it sets it back. In the finally block, you can see that the lock is deleted using the client.delete() method. This will remove the key from Couchbase and allow any other clients that are waiting to unregister to continue into the critical section one at a time.

It is now time to complete the functionality of the tutorial application by writing a thread that will output the messages that users type as well as a method of getting input from the users.

First add the following member variable to the class:

private static Thread messageThread;

Next, modify the main method again to add the following lines in bold:

if (register()) {
    startMessageThread();
    processInput();
    unregister();
    messageThread.interrupt();
}

Now we will need to write a few helper methods, the first is:

private static void printMessages(long startId, long endId) {

    for (long i = startId; i <= endId; i++) {
        String message = (String)client.get("Message:" + i);
        if (message != null)
            System.out.println(message);
    }

}

This method just iterates through a set of message numbers and prints the message to the screen. Couchbase does not allow iteration of keys, but that’s alright, we know exactly what pattern the key names follow, so we can do this.

The second method helps to find the oldest message that hasn’t expired in the cache, starting at the last message and running back toward the first message. Eventually it will find the first message and will return its number, considering that it will have run one past the end, it needs to do a little fix-up to return the correct number.

private static long findFirstMessage(long currentId) {
    CASValue<Object> cas = null;
    long firstId = currentId;
    do {
        firstId -= 1;
        cas = client.gets("Message:" + firstId);
    } while (cas != null);

    return firstId + 1;
}

Finally we come to the method that prints out all of the messages as they come in. It’s somewhat complicated so I’ll describe it in detail afterward.

private static void startMessageThread() {

    messageThread = new Thread(new Runnable() {
        public void run() {

            long messageId = -1;

            try {
                while (!Thread.interrupted()) {

                    CASValue<Object> msgCountCas = client.gets("Messages");

                    if (msgCountCas == null) {
                        Thread.sleep(250);
                        continue;
                    }

                    long current = Long.parseLong((String)msgCountCas.getValue());

                    if (messageId == -1) {
                        printMessages(findFirstMessage(current),
                                current);
                    } else if (current > messageId) {
                        printMessages(messageId + 1, current);
                    } else {
                        Thread.sleep(250);
                        continue;
                    }

                    messageId = current;

                }

            } catch (InterruptedException ex) {
            } catch (RuntimeException ex) {
            }

            System.out.println("Stopped message thread.");
        }
    });

    messageThread.start();

}

This code creates a new thread of execution and assigns it to the messageThread variable. It creates an anonymous Runnable class that implements a run() method inline.

The messageId variable is set to a sentinel value so that we know when it is the first time through the while loop. The while loop will iterate until the thread has been interrupted.

First, in the while loop, we write client.gets("Messages") which will return null if the value does not exist (in which case the loop sleeps for a little while and continues back to the top), or the method will return a CASValue<Object> instance that we can use to obtain the current message id.

If this is the first time through the loop (messageId == -1), we need to print out all of the messages since the first to the current.

Otherwise if the current messageId is bigger than what we’ve previously seen, it means that some new messages have come in since we last checked, so we will print them out.

Finally, nothing has changed since we last checked so just sleep some more.

At the end of the loop, we just make sure that the current message id is remembered for the next iteration of the loop. Exceptions are handled by suppressing them, and if the while loop exits we’ll print a message saying the message thread stopped.

At the end of the method, the thread is actually started.

Great, so, now if messages come in, we’ll display them. Also, when we first start the application, all of the messages stored in the cache will be displayed. We need to implement the actual method that allows the user to interact with the cache.

private static void processInput() {
    boolean quit = false;

    System.out.println("Enter text, or /who to see user list, or /quit to exit.");

    do {
        String input = System.console().readLine();
        if (input.startsWith("/quit")) {
            quit = true;
        } else if (input.startsWith("/who")) {
            System.out.println("Users connected: "
                    + client.get("CurrentUsers"));
        } else {
            // Send a new message to the chat
            long messageId = client.incr("Messages", 1, 1);
            client.set("Message:" + messageId, 3600,
                    getUserNameToken() + ": " + input);
        }

    } while (!quit);

}

The method keeps track of a quit variable to know when to exit the do/while loop, then prints out some simple instructions for the user.

The console is read one line at a time, and each is checked to see if it starts with a command. If the user has typed ‘/quit’ the quit flag will be set, and the loop will exit.

If the user has typed ‘/who’ the CurrentUsers cached value will be output to the screen, so that at any time a user can check who is currently online.

Otherwise, the line is treated as a message. Here we increment the Messages key and use that value as a message id. Then the client.set() method is called with a key of Message:MessageId with a timeout of one hour, followed by the user’s name and the text that they entered.

These changes to the cache will be noticed by the message thread, and output to the screen. Of course this means that each user will see his or her messages repeated back to them.

If you compile and run the program in multiple terminal windows, you can talk to yourself. This is about as fun as things can get, isn’t it? Notice how intelligent you can be.

Using Buckets¶

Up to this point, the test application has been using the default bucket. This is because it is not authenticated. The default bucket on Couchbase can be useful when you first start out, but as you build more complex applications, you may want to partition your data into different buckets to improve fault tolerance by boosting replication or just so that one bucket can be cleared without affecting all of the data you have cached in other buckets. You may also want to partition your key space among several applications to avoid naming collisions.

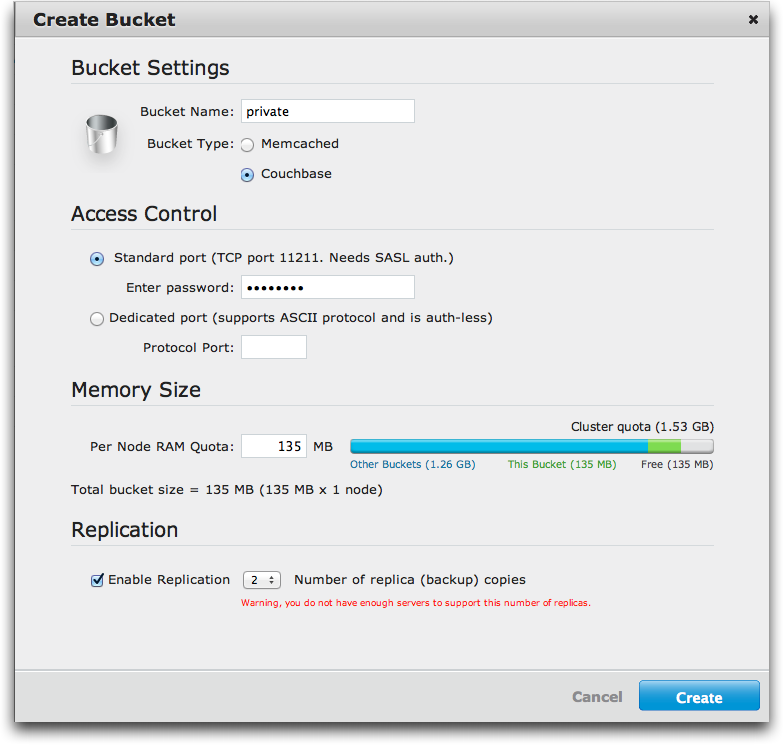
Figure 1 shows the dialog in the Couchbase Web Console that demonstrates creating a new bucket called private with two replicas. Here you also choose a password to protect the bucket during SASL authentication. How do you access this bucket? You have already learned about how to make a SASL authenticated connection to Couchbase, if you use the bucket name as the username, and the password you provided when creating the bucket, you will connect to the private bucket for data storage. The following code would accomplish this:

// We have used private as the username and private as the password
// but you would not do this, you would be much smarter and use
// something much harder to guess.
    CouchbaseConnectionFactory cf = new CouchbaseConnectionFactory(baseURIs,
       "private", "private");
     client = new CouchbaseClient((CouchbaseConnectionFactory) cf);

Error Handling¶

At this point, you may still be wondering how CAS values are used to prevent clients from writing over values that were changed by another client.

In essence, the CAS value exists so that that a client can ‘hold’ the CAS value for a item ID that it knows, and only update the item if the CAS has not changed. Hence, Check And Set (CAS). In a multi-client environment it’s designed to prevent one client changing the value of an item when another client may have already updated it.

Unfortunately there’s no way to lock items; individual operations (set, for example) are atomic, but multiple operations are not, and this is what CAS is designed to protect against. To stop you changing a value that has changed since the last GET.

In order to demonstrate this situation, add the bold lines to the processInput method to allow a way to perform a CAS operation and see what happens if two of these operations is interleaved if two copies of the program are run at the same time.

} else if (input.startsWith("/who")) {
    System.out.println("Users connected: "
            + client.get("CurrentUsers"));
} else if (input.startsWith("/cas")) {
    runCasTest();
} else {

Now create the runCasTest() method at the bottom of the class:

private static void runCasTest() {

    System.out.println("Testing a CAS operation.");
    CASValue<Object> cas = client.gets("CasTest");

    if (cas == null) {
        // Must create it first
        System.out.println("Creating CasTest value.");
        client.set("CasTest", 120, "InitialValue");
        return;
    }

    System.out.println("CAS for CasTest = "+cas.getCas());
    System.out.println("Sleeping for 10 seconds.");
    try {
        Thread.sleep(10000);
    } catch (InterruptedException e) {
    }

    CASResponse response =
        client.cas("CasTest", cas.getCas(), "ReplacedValue");
    if (response.equals(CASResponse.OK)) {
        System.out.println("OK response.");
    }
    else if (response.equals(CASResponse.EXISTS)) {
        System.out.println("EXISTS response.");
    }
    else if (response.equals(CASResponse.NOT_FOUND)) {
        System.out.println("NOT_FOUND response.");
    }

    cas = client.gets("CasTest");
    System.err.println("CAS after = "+cas.getCas());
}

The first time the test is run (by typing “/cas” while the application is running) the gets() method will return null so it will just set the CasTest key to “InitialValue” and return. The second time the test is run it will get a CASValue<Object> instance from the gets() method, print out its value, and then sleep for 10 seconds. Then after sleeping the code performs a client.cas() method call to replace the value.

If you run this in two different windows you may see output something like the following if you time things just right:

/cas
/cas
Testing a CAS operation.
CAS for CasTest = 2637312854241
Sleeping for 10 seconds.
OK response.
CAS after = 2850841875395

In the second copy of the application, the output would look something like this:

Testing a CAS operation.
CAS for CasTest = 2637312854241
Sleeping for 10 seconds.
EXISTS response.
CAS after = 2850841875395

What you see is that when the CAS is 2637312854241, the second client modifies the value before the first client is done sleeping. Instead of getting an OK response, that client gets an EXISTS response indicating that a change has been made before it had a chance to do so, so its client.cas() operation failed, and the code would have to handle this situation to rectify the situation.

Locking is not an option if you want to have an operational distributed cache. Locking causes contention and complexity. Being able to quickly detect when a value has been overwritten without having to hold a lock is a simple solution to the problem. You will be able to write code to handle the situation either by returning an error to the user, or retrying the operation after obtaining another CAS value.

Using Couchbase Cluster¶

One of the newest features of the Couchbase SDKs and spymemcached libraries is the support for communicating intelligently with the Couchbase Server cluster. The smart client support allows the SDK to automatically connect clients to the data stored within the cluster by directly communicating with the right node in the cluster. This ability also allows for clints to continue to operate during failover and rebalancing operations.

All you need to start using this functionality is to use a new Couchbase constructor that allows you to pass in a list of base URIs, and the bucket name and password as we did in the connect() method earlier.

try {
    URI server = new URI(addresses);
    ArrayList<URI> serverList = new ArrayList<URI>();
    serverList.add(server);
    CouchbaseClient client = new CouchbaseClient(
            serverList, "rags", "password");
} catch (Throwable ex) {
    ex.printStackTrace();
}

Compile and run the application:

shell> javac -cp couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar Tutorial.java
shell> java -cp .:couchbase-client-1.0.0.jar:\
spymemcached-2.8.0.jar:jettison-1.1.jar:netty-3.2.0.Final.jar:\
commons-codec-1.5.jar Tutorial 192.168.3.104

Replace serverhost with the name or IP address of your server, you won’t need the port this time. You will see something like the following output:

Jan 17, 2012 12:11:43 PM net.spy.memcached.MemcachedConnection createConnections
INFO: Added {QA sa=/192.168.3.111:11210, #Rops=0, #Wops=0, #iq=0, topRop=null, topWop=null, toWrite=0, interested=0} to connect queue
Jan 17, 2012 12:11:43 PM net.spy.memcached.MemcachedConnection handleIO
INFO: Connection state changed for sun.nio.ch.SelectionKeyImpl@2abe0e27
Jan 17, 2012 12:11:43 PM net.spy.memcached.auth.AuthThread$1 receivedStatus
INFO: Authenticated to /192.168.3.111:11210

You can see that it connects to the server and automatically loads the list of all Couchbase servers, connects to them and authenticates. It uses the vbucket algorithm automatically, and no code changes to the application will be required.

The Tutorial Example Code¶

The Complete code for the tutorial is below and you would compile and run it with the command line arguments as below ensuring that the client libraries are included in the Java classpath.

shell> javac -cp couchbase-client-1.0.0.jar:spymemcached-2.8.0.jar Tutorial.java
shell> java -cp .:couchbase-client-1.0.0.jar:\
spymemcached-2.8.0.jar:jettison-1.1.jar:netty-3.2.0.Final.jar:\
commons-codec-1.5.jar Tutorial 192.168.3.104

import java.io.IOException;
import java.net.SocketAddress;
import java.net.URI;
import java.net.URISyntaxException;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.concurrent.Future;
import java.util.concurrent.TimeUnit;

import javax.naming.ConfigurationException;

import net.spy.memcached.CASMutation;
import net.spy.memcached.CASMutator;
import net.spy.memcached.CASResponse;
import net.spy.memcached.CASValue;
import net.spy.memcached.CachedData;
import net.spy.memcached.ConnectionObserver;
import net.spy.memcached.transcoders.SerializingTranscoder;
import net.spy.memcached.transcoders.Transcoder;

import com.couchbase.client.CouchbaseClient;
import com.couchbase.client.CouchbaseConnectionFactory;

public class Tutorial {

    private static CouchbaseClient client;
    private long userId = 0;
    private long userCount = 0;
    private Thread messageThread;

    /**
     * Main Program for a Couchbase chat room application using
     * the couchbase-client and spymemcached libraries.
     */
    public static void main(String[] args) {

        if (args.length != 1) {
            System.err.println("usage: serveraddresses");
            System.exit(1);
        }

        try {

            new Tutorial().run(args[0]);

        } catch (Exception ex) {
            System.err.println(ex);
            client.shutdown();
        }
    }

    public void run(String serverAddress) throws Exception {

        System.setProperty("net.spy.log.LoggerImpl",
            "net.spy.memcached.compat.log.SunLogger");

        System.out.println(String
                .format("Connecting to %s", serverAddress));

        connect(serverAddress);

        if (register()) {
            startMessageThread();
            Runtime.getRuntime().addShutdownHook(new unregisterThread());
            processInput();
            unregister();
            messageThread.interrupt();
        }
        client.shutdown(1, TimeUnit.MINUTES);
        System.exit(0);
    }

    /**
     * Connect to the server, or servers given.
     * @param serverAddress the server addresses to connect with.
     * @throws IOException if there is a problem with connecting.
     * @throws URISyntaxException
     * @throws ConfigurationException
     */
    private void connect(String serverAddress) throws Exception {

        URI base = new URI(
                String.format("http://%s:8091/pools",serverAddress));
        List<URI> baseURIs = new ArrayList<URI>();
        baseURIs.add(base);
        CouchbaseConnectionFactory cf = new
                CouchbaseConnectionFactory(baseURIs, "default", "");

        client = new CouchbaseClient((CouchbaseConnectionFactory) cf);

        client.addObserver(new ConnectionObserver() {

            public void connectionLost(SocketAddress sa) {
                System.out.println("Connection lost to " + sa.toString());
            }

            public void connectionEstablished(SocketAddress sa,
                    int reconnectCount) {
                System.out.println("Connection established with "
                        + sa.toString());
                System.out.println("Reconnected count: " + reconnectCount);
            }
        });

    }

    /**
     * Get a user name token for the current user.
     * @return the token to use.
     */
    private String getUserNameToken() {
        return String.format("<User-%d>", userId);
    }

    /**
     * Register the user with the chat room.
     * @return true if the registration succeeded, false otherwise.
     */
    private boolean register() throws Exception {

        userId = client.incr("UserId", 1, 1);
        System.out.println("You are user " + userId + ".");

        CASValue<Object> casValue = client.gets("CurrentUsers");

        if (casValue == null) {

            System.out.println("First user ever!");

            client.set("CurrentUsers", Integer.MAX_VALUE,
                    getUserNameToken()).get();

        } else {

            Future<Boolean> appendDone = client.append(casValue.getCas(),
                    "CurrentUsers", getUserNameToken());

            if (appendDone.get()) {
                System.out.println("Registration succeeded.");
            } else {
                System.out.println("Sorry registration failed.");
                return false;
            }

        }

        userCount = client.incr("UserCount", 1, 1);
        System.out.println("There are currently " + userCount
                + " connected.");

        return true;
    }

    /**
     * A Transcoder for strings that just delegates to using
     * a SerializingTranscoder.
     */
    class StringTranscoder implements Transcoder<String> {

        final SerializingTranscoder delegate = new SerializingTranscoder();

        public boolean asyncDecode(CachedData d) {
            return delegate.asyncDecode(d);
        }

        public String decode(CachedData d) {
            return (String)delegate.decode(d);
        }

        public CachedData encode(String o) {
            return delegate.encode(o);
        }

        public int getMaxSize() {
            return delegate.getMaxSize();
        }

    }

    /**
     * Unregister the current user from the chat room.
     */
    private void unregister() throws Exception {

        CASMutation<String> mutation = new CASMutation<String>() {
            public String getNewValue(String current) {
                return current.replaceAll(getUserNameToken(), "");
            }
        };

        Transcoder<String> transcoder = new StringTranscoder();
        CASMutator<String> mutator = new CASMutator<String>(client, transcoder);
        mutator.cas("CurrentUsers", "", 0, mutation);

        client.decr("UserCount", 1);
        System.out.println("Unregistered.");

    }

    /**
     * Print a number of messages.
     * @param startId the first message id to output.
     * @param endId the last message id to output.
     */
    private void printMessages(long startId, long endId) {

        for (long i = startId; i <= endId; i++) {
            String message = (String)client.get("Message:" + i);
            if (message != null)
                System.out.println(message);
        }

    }

    /**
     * Finds the first message id that has not yet expired.
     * @param currentId the last message id to start with.
     * @return the first message id known in the system at the time.
     */
    private long findFirstMessage(long currentId) {
        CASValue<Object> cas = null;
        long firstId = currentId;
        do {
            firstId -= 1;
            cas = client.gets("Message:" + firstId);
        } while (cas != null);

        return firstId + 1;
    }

    /**
     * Start up the message display thread.
     */
    private void startMessageThread() {

        messageThread = new Thread(new Runnable() {
            public void run() {

                long messageId = -1;

                try {
                    while (!Thread.interrupted()) {

                        CASValue<Object> msgCountCas = client
                                .gets("Messages");

                        if (msgCountCas == null) {
                            Thread.sleep(250);
                            continue;
                        }

                        long current = Long.parseLong((String)msgCountCas
                                .getValue());

                        if (messageId == -1) {
                            printMessages(findFirstMessage(current),
                                    current);
                        } else if (current > messageId) {
                            printMessages(messageId + 1, current);
                        } else {
                            Thread.sleep(250);
                            continue;
                        }

                        messageId = current;

                    }

                } catch (InterruptedException ex) {
                } catch (RuntimeException ex) {
                }

                System.out.println("Stopped message thread.");
            }
        });

        messageThread.start();
    }

    /**
     * Handle shutdown by unregistering
     */
    private class unregisterThread extends Thread {


    public void run() {
      try {

        unregister();
        messageThread.interrupt();
        client.shutdown(1, TimeUnit.MINUTES);
        super.run();;
      } catch (Exception e) {
      }
    }
  }

    /**
     * Processes input from the user, and sends messages to the virtual
     * chat room.
     */
    private void processInput() {
        boolean quit = false;

        System.out.
          println("Enter text, or /who to see user list, or /quit to exit.");

        try {
        do {
            String input = System.console().readLine();
            System.out.println(input);
            if (input.startsWith("/quit")) {
                quit = true;
            } else if (input.startsWith("/who")) {
                System.out.println("Users connected: "
                        + client.get("CurrentUsers"));
            } else if (input.startsWith("/cas")) {
                runCasTest();
            } else {
                // Send a new message to the chat
                long messageId = client.incr("Messages", 1, 1);
                client.set("Message:" + messageId, 3600,
                        getUserNameToken() + ": " + input);
            }

        } while (!quit);
        } catch (Exception e) {
        }

    }

    private void runCasTest() {
        System.out.println("Testing a CAS operation.");
        CASValue<Object> cas = client.gets("CasTest");

        if (cas == null) {
            // Must create it first
            System.out.println("Creating CasTest value.");
            client.set("CasTest", 120, "InitialValue");
            return;
        }

        System.out.println("CAS for CasTest = "+cas.getCas());
        System.out.println("Sleeping for 10 seconds.");
        try {
            Thread.sleep(10000);
        } catch (InterruptedException e) {
        }

        CASResponse response =
            client.cas("CasTest", cas.getCas(), "ReplacedValue");
        if (response.equals(CASResponse.OK)) {
            System.out.println("OK response.");
        }
        else if (response.equals(CASResponse.EXISTS)) {
            System.out.println("EXISTS response.");
        }
        else if (response.equals(CASResponse.NOT_FOUND)) {
            System.out.println("NOT_FOUND response.");
        }

        cas = client.gets("CasTest");
        System.err.println("CAS after = "+cas.getCas());
    }
}

Congratulations, you have completed the Couchbase portion of this tutorial. You can download the entire Java Tutorial Source code and follow along with the steps.

Using the APIs¶

The Client libraries provides an interface to both Couchbase and Memcached clients using a consistent interface. The interface between your Java application and your Couchbase or Memcached servers is provided through the instantiation of a single object class, CouchbaseClient.

Creating a new object based on this class opens the connection to each configured server and handles all the communication with the server(s) when setting, retrieving and updating values. A number of different methods are available for creating the object specifying the connection address and methods.

Connecting to a Couchbase Bucket¶

You can connect to specific Couchbase buckets (in place of using the default bucket, or a hostname/port combination configured on the Couchbase cluster) by using the Couchbase URI for one or more Couchbase nodes, and specifying the bucket name and password (if required) when creating the new CouchbaseClient object.

For example, to connect to the local host and the default bucket:

List<URI> uris = new LinkedList<URI>();

    uris.add(URI.create("http://127.0.0.1:8091/pools"));
    try {
      client = new CouchbaseClient(uris, "default", "");
    } catch (Exception e) {
      System.err.println("Error connecting to Couchbase: " + e.getMessage());
      System.exit(0);
    }

The format of this constructor is:

CouchbaseClient(URIs,BUCKETNAME,BUCKETPASSWORD)

Where:

• URIS is a List of URIs to the Couchbase nodes. The format of the URI is the hostname, port and path /pools.

• BUCKETNAME is the name of the bucket on the cluster that you want to use. Specified as a String.

• BUCKETPASSWORD is the password for this bucket. Specified as a String.

The returned CouchbaseClient object can be used as with any other CouchbaseClient object.

Connecting using Hostname and Port with SASL¶

If you want to use SASL to provide secure connectivity to your Couchbase server then you could create a CouchbaseConnectionFactory that defines the SASL connection type, userbucket and password.

The connection to Couchbase uses the underlying protocol for SASL. This is similar to the earlier example except that we use the CouchbaseConnectionFactory.

List<URI> baseURIs = new ArrayList<URI>();
        baseURIs.add(base);
        CouchbaseConnectionFactory cf = new
                CouchbaseConnectionFactory(baseURIs,
                    "userbucket", "password");

        client = new CouchbaseClient((CouchbaseConnectionFactory) cf);

Shutting down the Connection¶

The preferred method for closing a connection is to cleanly shutdown the active connection with a timeout using the shutdown() method with an optional timeout period and unit specification. The following will shutdown the active connection to all the configured servers after 60 seconds:

client.shutdown(60, TimeUnit.SECONDS);

The unit specification relies on the TimeUnit object enumerator, which supports the following values:

Constant	Description
TimeUnit.NANOSECONDS	Nanoseconds (10 -9 s).
TimeUnit.MICROSECONDS	Microseconds (10 -6 s).
TimeUnit.MILLISECONDS	Milliseconds (10 -3 s).
TimeUnit.SECONDS	Seconds.

The method returns a boolean value indicating whether the shutdown request completed successfully.

You also can shutdown an active connection immediately by using the shutdown() method to your Couchbase object instance. For example:

client.shutdown();

In this form the shutdown() method returns no value.

Java Method Summary¶

The couchbase-client and spymemcached libraries support the full suite of API calls to Couchbase.

Synchronous Method Calls¶

The Java Client Libraries support the core Couchbase API methods as direct calls to the Couchbase server through the API call. These direct methods can be used to provide instant storage, retrieval and updating of Couchbase key/value pairs.

For example, the following fragment stores and retrieves a single key/value pair:

client.set("someKey", 3600, someObject);

Object myObject = client.get("someKey");

In the example code above, the client get() call will wait until a response has been received from the appropriately configured Couchbase servers before returning the required value or an exception.

Asynchronous Method Calls¶

In addition, the librares also support a range of asynchronous methods that can be used to store, update and retrieve values without having to explicitly wait for a response.

The asynchronous methods use a Future object or its appropriate implementation which is returned by the initial method call for the operation. The communication with the Couchbase server will be handled by the client libraries in the background so that the main program loop can continue. You can recover the status of the operation by using a method to check the status on the returned Future object. For example, rather than synchronously getting a key, an asynchronous call might look like this:

GetFuture getOp = client.asyncGet("someKey");

This will populate the Future object GetFuture with the response from the server. The Future object class is defined here. The primary methods are:

• cancel()

  Attempts to Cancel the operation if the operation has not already been completed.

• get()

  Waits for the operation to complete. Gets the object returned by the operation as if the method was synchronous rather than asynchronous.

• get(timeout, TimeUnit)

  Gets the object waiting for a maximum time specified by timeout and the corresponding TimeUnit.

• isDone()

  The operation has been completed successfully.

For example, you can use the timeout method to obtain the value or cancel the operation:

GetFuture getOp = client.asyncGet("someKey");

Object myObj;

try {
    myObj = getOp.get(5, TimeUnit.SECONDS);
} catch(TimeoutException e) {
    getOp.cancel(false);
}

Alternatively, you can do a blocking wait for the response by using the get() method:

Object myObj;

myObj = getOp.get();

Object Serialization (Transcoding)¶

All of the Java client library methods use the default Whalin transcoder that provides compatilibility with memcached clients for the serialization of objects from the object type into a byte array used for storage within Couchbase.

You can also use a custom transcoder the serialization of objects. This can be to serialize objects in a format that is compatible with other languages or environments.

You can customize the transcoder by implementing a new Transcoder interface and then using this when storing and retrieving values. The Transcoder will be used to encode and decode objects into binary strings. All of the methods that store, retrieve or update information have a version that supports a custom transcoder.

Expiry Values¶

All values in Couchbase and Memcached can be set with an expiry value. The expiry value indicates when the item should be expired from the database and can be set when an item is added or updated.

Within spymemcached the expiry value is expressed in the native form of an integer as per the Memcached protocol specification. The integer value is expressed as the number of seconds, but the interpretation of the value is different based on the value itself:

• Expiry is less than 30*24*60*60 (30 days)

  The value is interpreted as the number of seconds from the point of storage or update.

• Expiry is greater than 30*24*60*60

  The value is interpreted as the number of seconds from the epoch (January 1st, 1970).

• Expiry is 0

  This disables expiry for the item.

For example:

client.set("someKey", 3600, someObject);

The value will have an expiry time of 3600 seconds (one hour) from the time the item was stored.

The statement:

client.set("someKey", 1307458800, someObject);

Will set the expiry time as June 7th 2011, 15:00 (UTC).

Connection Operations¶

API Call	client.new CouchbaseClient([ url ] [, urls ] [, username ] [, password ])
Asynchronous	no
Description	Create a connection to Couchbase Server with given parameters, such as node URL. The connection obtains the cluster configuration from the first host to which it has connected. Further communication operates directly with each node in the cluster as required.
Returns	(none)
Arguments
String url	URL for Couchbase Server Instance, or node.
String urls	Linked list containing one or more URLs as strings.
String username	Username for Couchbase bucket.
String password	Password for Couchbase bucket.

Store Operations¶

The Couchbase Java Client Library store operations set information within the Couchbase database. These are distinct from the update operations in that the key does not have to exist within the Couchbase database before being stored.

Add Operations¶

The add() method adds a value to the database with the specified key, but will fail if the key already exists in the database.

API Call	client.add(key, expiry, value)
Asynchronous	yes
Description	Add a value with the specified key that does not already exist. Will fail if the key/value pair already exist.
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored

The add() method adds a value to the database using the specified key.

client.add("someKey", 0, someObject);

Unlike Set Operations the operation can fail (and return false) if the specified key already exist.

For example, the first operation in the example below may complete if the key does not already exist, but the second operation will always fail as the first operation will have set the key:

OperationFuture<Boolean> addOp = client.add("someKey",0,"astring");
System.out.printf("Result was %b",addOp.get());
addOp =  client.add("someKey",0,"anotherstring");
System.out.printf("Result was %b",addOp.get());

API Call	client.add(key, expiry, value, transcoder)
Asynchronous	yes
Description	Add a value with the specified key that does not already exist. Will fail if the key/value pair already exist.
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

This method is identical to the add() method, but supports the use of a custom transcoder for serialization of the object value. For more information on transcoding, see Object Serialization (Transcoding).

Set Operations¶

The set operations store a value into Couchbase or Memcached using the specified key and value. The value is stored against the specified key, even if the key already exists and has data. This operation overwrites the existing with the new data.

API Call	client.set(key, expiry, value)
Asynchronous	yes
Description	Store a value using the specified key, whether the key already exists or not. Will overwrite a value if the given key/value already exists.
Returns	OperationFuture<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored

The first form of the set() method stores the key, sets the expiry (use 0 for no expiry), and the corresponding object value using the built in transcoder for serialization.

The simplest form of the command is:

client.set("someKey", 3600, someObject);

The Boolean return value will be true if the value was stored. For example:

OperationFuture<Boolean> setOp = membase.set("someKey",0,"astring");
System.out.printf("Result was %b",setOp.get());

API Call	client.set(key, expiry, value, transcoder)
Asynchronous	yes
Description	Store a value using the specified key and a custom transcoder.
Returns	OperationFuture<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

This method is identical to the set() method, but supports the use of a custom transcoder for serialization of the object value. For more information on transcoding, see Object Serialization (Transcoding).

Retrieve Operations¶

The retrieve operations get information from the Couchbase database. A summary of the available API calls is listed below.

Synchronous get Methods¶

The synchronous get() methods allow for direct access to a given key/value pair.

API Call	client.get(key)
Asynchronous	no
Description	Get one or more key values
Returns	Object ( Binary object )
Arguments
String key	Document ID used to identify the value

The get() method obtains an object stored in Couchbase using the default transcoder for serialization of the object.

For example:

Object myObject = client.get("someKey");

Transcoding of the object assumes the default transcoder was used when the value was stored. The returned object can be of any type.

If the request key does no existing in the database then the returned value is null.

API Call	client.get(key, transcoder)
Asynchronous	no
Description	Get one or more key values
Returns	T ( Transcoded object )
Arguments
String key	Document ID used to identify the value
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the get() retrieves a value from Couchbase using a custom transcoder.

For example to obtain an integer value using the IntegerTranscoder:

Transcoder<Integer> tc = new IntegerTranscoder();
Integer ic = client.get("someKey", tc);

Asynchronous get Methods¶

The asynchronous asyncGet() methods allow to retrieve a given value for a key without waiting actively for a response.

API Call	client.asyncGet(key)
Asynchronous	yes
Description	Get one or more key values
Returns	Future<Object> ( Asynchronous request value, as Object )
Arguments
String key	Document ID used to identify the value
Exceptions
TimeoutException	Value could not be retrieved

The first form of the asyncGet() method obtains a value for a given key returning a Future object so that the value can be later retrieved. For example, to get a key with a stored String value:

GetFuture<Object> getOp =
    client.asyncGet("samplekey");

String username;

try {
    username = (String) getOp.get(5, TimeUnit.SECONDS);
} catch(Exception e) {
    getOp.cancel(false);
}

API Call	client.asyncGet(key, transcoder)
Asynchronous	yes
Description	Get one or more key values
Returns	Future<T> ( Asynchronous request value, as Transcoded Object )
Arguments
String key	Document ID used to identify the value
Transcoder transcoder	Transcoder class to be used to serialize value

The second form is identical to the first, but includes the ability to use a custom transcoder on the stored value.

Get-and-Touch Methods¶

The Get-and-Touch (GAT) methods obtain a value for a given key and update the expiry time for the key. This can be useful for session values and other information where you want to set an expiry time, but don’t want the value to expire while the value is still in use.

API Call	client.getAndTouch(key, expiry)
Asynchronous	no
Description	Get a value and update the expiration time for a given key
Introduced Version	1.0
Returns	CASValue ( Check and set object )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).

The first form of the getAndTouch() obtains a given value and updates the expiry time. For example, to get session data and renew the expiry time to five minutes:

session = client.getAndTouch("sessionid",300);

API Call	client.getAndTouch(key, expiry, transcoder)
Asynchronous	no
Description	Get a value and update the expiration time for a given key
Introduced Version	1.0
Returns	CASValue ( Check and set object )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Transcoder transcoder	Transcoder class to be used to serialize value

The second form supports the use of a custom transcoder for the stored value information.

API Call	client.asyncGetAndTouch(key, expiry)
Asynchronous	yes
Description	Get a value and update the expiration time for a given key
Introduced Version	1.0
Returns	Future<CASValue<Object>> ( Asynchronous request value, as CASValue, as Object )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).

The asynchronous methods obtain the value and update the expiry time without requiring you to actively wait for the response. The returned value is a CAS object with the embedded value object.

Future<CASValue<Object>> future = client.asyncGetAndTouch("sessionid", 300);

CASValue casv;

try {
    casv = future.get(5, TimeUnit.SECONDS);
} catch(Exception e) {
    future.cancel(false);
}

API Call	client.asyncGetAndTouch(key, expiry, transcoder)
Asynchronous	yes
Description	Get a value and update the expiration time for a given key
Introduced Version	1.0
Returns	Future<CASValue<T>> ( Asynchronous request value, as CASValue as Transcoded object )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the asynchronous method supports the use of a custom transcoder for the stored object.

CAS get Methods¶

The gets() methods obtain a CAS value for a given key. The CAS value is used in combination with the corresponding Check-and-Set methods when updating a value. For example, you can use the CAS value with the append() operation to update a value only if the CAS value you supply matches. For more information see Append Methods and Check-and-Set Methods.

API Call	client.gets(key)
Asynchronous	no
Description	Get single key value with CAS value
Returns	CASValue ( Check and set object )
Arguments
String key	Document ID used to identify the value

The gets() method obtains a CASValue for a given key. The CASValue holds the CAS to be used when performing a Check-And-Set operation, and the corresponding value for the given key.

For example, to obtain the CAS and value for the key someKey :

CASValue status = client.gets("someKey");
System.out.printf("CAS is %s\n",status.getCas());
System.out.printf("Result was %s\n",status.getValue());

The CAS value can be used in a CAS call such as append() :

client.append(status.getCas(),"someKey", "appendedstring");

API Call	client.gets(key, transcoder)
Asynchronous	no
Description	Get single key value with CAS value
Returns	CASValue ( Check and set object )
Arguments
String key	Document ID used to identify the value
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the gets() method supports the use of a custom transcoder.

API Call	client.asyncGets(key)
Asynchronous	yes
Description	Get single key value with CAS value
Returns	Future<CASValue<Object>> ( Asynchronous request value, as CASValue, as Object )
Arguments
String key	Document ID used to identify the value

The asyncGets() method obtains the CASValue object for a stored value against the specified key, without requiring an explicit wait for the returned value.

For example:

Future<CASValue<Object>> future = client.asyncGets("someKey");

System.out.printf("CAS is %s\n",future.get(5,TimeUnit.SECONDS).getCas());

Note that you have to extract the CASValue from the Future response, and then the CAS value from the corresponding object. This is performed here in a single statement.

API Call	client.asyncGets(key, transcoder)
Asynchronous	yes
Description	Get single key value with CAS value
Returns	Future<CASValue<T>> ( Asynchronous request value, as CASValue as Transcoded object )
Arguments
String key	Document ID used to identify the value
Transcoder transcoder	Transcoder class to be used to serialize value

The final form of the asyncGets() method supports the use of a custom transcoder.

Bulk get Methods¶

The bulk getBulk() methods allow you to get one or more items from the database in a single request. Using the bulk methods is more efficient than multiple single requests as the operation can be conducted in a single network call.

API Call	client.getBulk(keycollection)
Asynchronous	no
Description	Get one or more key values
Returns	Map<String,Object> ( Map of Strings/Objects )
Arguments
Collection keycollection	One or more keys used to reference a value

The first format accepts a String Collection as the request argument which is used to specify the list of keys that you want to retrieve. The return type is Map between the keys and object values.

For example:

Map<String,Object> keyvalues = client.getBulk(keylist);

System.out.printf("A is %s\n",keyvalues.get("keyA"));
System.out.printf("B is %s\n",keyvalues.get("keyB"));
System.out.printf("C is %s\n",keyvalues.get("keyC"));

The returned map will only contain entries for keys that exist from the original request. For example, if you request the values for three keys, but only one exists, the resultant map will contain only that one key/value pair.

API Call	client.getBulk(keycollection, transcoder)
Asynchronous	no
Description	Get one or more key values
Returns	Map<String,T> ( Map of Strings/Transcoded objects )
Arguments
Collection keycollection	One or more keys used to reference a value
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the getBulk() method supports the same Collection argument, but also supports the use of a custom transcoder on the returned values.

The specified transcoder will be used for every value requested from the database.

API Call	client.getBulk(keyn)
Asynchronous	no
Description	Get one or more key values
Returns	Map<String,Object> ( Map of Strings/Objects )
Arguments
String… keyn	One or more keys used to reference a value

The third form of the getBulk() method supports a variable list of arguments with each interpreted as the key to be retrieved from the database.

For example, the equivalent of the Collection method operation using this method would be:

Map<String,Object> keyvalues = client.getBulk("keyA","keyB","keyC");

System.out.printf("A is %s\n",keyvalues.get("keyA"));
System.out.printf("B is %s\n",keyvalues.get("keyB"));
System.out.printf("C is %s\n",keyvalues.get("keyC"));

The return Map will only contain entries for keys that exist. Non-existent keys will be silently ignored.

API Call	client.getBulk(transcoder, keyn)
Asynchronous	no
Description	Get one or more key values
Returns	Map<String,T> ( Map of Strings/Transcoded objects )
Arguments
Transcoder transcoder	Transcoder class to be used to serialize value
String… keyn	One or more keys used to reference a value

The fourth form of the getBulk() method uses the variable list of arguments but supports a custom transcoder.

Note that unlike other formats of the methods used for supporting custom transcoders, the transcoder specification is at the start of the argument list, not the end.

API Call	client.asyncGetBulk(keycollection)
Asynchronous	yes
Description	Get one or more key values
Returns	BulkFuture<Map<String,Object>> ( Map of Strings/Objects )
Arguments
Collection keycollection	One or more keys used to reference a value

The asynchronous getBulk() method supports a Collection of keys to be retrieved, returning a BulkFuture object (part of the spymemcached package) with the returned map of key/value information. As with other asynchronous methods, the benefit is that you do not need to actively wait for the response.

The BulkFuture object operates slightly different in context to the standard Future object. Whereas the Future object gets a returned single value, the BulkFuture object will return an object containing as many keys as have been returned. For very large queries requesting large numbers of keys this means that multiple requests may be required to obtain every key from the original list.

For example, the code below will obtain as many keys as possible from the supplied Collection.

BulkFuture<Map<String,Object>> keyvalues = membase.asyncGetBulk(keylist);

Map<String,Object> keymap = keyvalues.getSome(5,TimeUnit.SECONDS);

System.out.printf("A is %s\n",keymap.get("keyA"));
System.out.printf("B is %s\n",keymap.get("keyB"));
System.out.printf("C is %s\n",keymap.get("keyC"));

API Call	client.asyncGetBulk(keycollection, transcoder)
Asynchronous	yes
Description	Get one or more key values
Returns	BulkFuture<Map<String,T>> ( Map of Strings/Transcoded objects )
Arguments
Collection keycollection	One or more keys used to reference a value
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the asynchronous getBulk() method supports the custom transcoder for the returned values.

API Call	client.asyncGetBulk(keyn)
Asynchronous	yes
Description	Get one or more key values
Returns	BulkFuture<Map<String,Object>> ( Map of Strings/Objects )
Arguments
String… keyn	One or more keys used to reference a value

The third form is identical to the multi-argument key request method (seecollection based asyncBulkGet() ), except that the operation occurs asynchronously.

API Call	client.asyncGetBulk(transcoder, keyn)
Asynchronous	yes
Description	Get one or more key values
Returns	BulkFuture<Map<String,T>> ( Map of Strings/Transcoded objects )
Arguments
Transcoder transcoder	Transcoder class to be used to serialize value
String… keyn	One or more keys used to reference a value

The final form of the asyncGetBulk() method supports a custom transcoder with the variable list of keys supplied as arguments.

Get and Lock¶

API Call	client.getAndLock(key [, getl-expiry ])
Asynchronous	yes
Description	Get the value for a key, lock the key from changes
Returns	CASValue<Object> ( CASValue as Object )
Arguments
String key	Document ID used to identify the value
int getl-expiry	Expiry time for lock
	Default
	Maximum
Exceptions
OperationTimeoutException	Exception timeout occured while waiting for value.
RuntimeException	Exception object specifying interruption while waiting for value.

Unlock¶

API Call	client.unlock(key, casunique)
Asynchronous	no
Description	Unlock a previously locked key by providing the corresponding CAS value that was returned during the lock
Returns	Boolean ( Boolean (true/false) )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
Exceptions
InterruptedException	Interrupted Exception while waiting for value.
OperationTimeoutException	Exception timeout occured while waiting for value.
RuntimeException	Exception object specifying interruption while waiting for value.

Unlock is supported with the couchbase-client library 1.0.2 onwards.

Update Operations¶

The update methods support different methods of updating and changing existing information within Couchbase. A list of the available methods is listed below.

Append Methods¶

The append() methods allow you to add information to an existing key/value pair in the database. You can use this to add information to a string or other data after the existing data.

The append() methods append raw serialized data on to the end of the existing data in the key. If you have previously stored a serialized object into Couchbase and then use append, the content of the serialized object will not be extended. For example, adding an Array of integers into the database, and then using append() to add another integer will result in the key referring to a serialized version of the array, immediately followed by a serialized version of the integer. It will not contain an updated array with the new integer appended to it. De-serialization of objects that have had data appended may result in data corruption.

API Call	client.append(casunique, key, value)
Asynchronous	no
Description	Append a value to an existing key
Returns	Object ( Binary object )
Arguments
long casunique	Unique value used to verify a key/value combination
String key	Document ID used to identify the value
Object value	Value to be stored

The append() appends information to the end of an existing key/value pair. The append() function requires a CAS value. For more information on CAS values, see CAS get Methods.

For example, to append a string to an existing key:

CASValue<Object> casv = client.gets("samplekey");
client.append(casv.getCas(),"samplekey", "appendedstring");

You can check if the append operation succeeded by using the return OperationFuture value:

OperationFuture<Boolean> appendOp =
    client.append(casv.getCas(),"notsamplekey", "appendedstring");

try {
    if (appendOp.get().booleanValue()) {
        System.out.printf("Append succeeded\n");
    }
    else {
        System.out.printf("Append failed\n");
    }
}
catch (Exception e) {
...
}

API Call	client.append(casunique, key, value, transcoder)
Asynchronous	no
Description	Append a value to an existing key
Returns	Object ( Binary object )
Arguments
long casunique	Unique value used to verify a key/value combination
String key	Document ID used to identify the value
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the append() method supports the use of custom transcoder.

Prepend Methods¶

The prepend() methods insert information before the existing data for a given key. Note that as with the append() method, the information will be inserted before the existing binary data stored in the key, which means that serialization of complex objects may lead to corruption when using prepend().

API Call	client.prepend(casunique, key, value)
Asynchronous	yes
Description	Prepend a value to an existing key
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
long casunique	Unique value used to verify a key/value combination
String key	Document ID used to identify the value
Object value	Value to be stored

The prepend() inserts information before the existing data stored in the key/value pair. The prepend() function requires a CAS value. For more information on CAS values, see CAS get Methods.

For example, to prepend a string to an existing key:

CASValue<Object> casv = client.gets("samplekey");
client.prepend(casv.getCas(),"samplekey", "prependedstring");

You can check if the prepend operation succeeded by using the return OperationFuture value:

OperationFuture<Boolean> prependOp =
    client.prepend(casv.getCas(),"notsamplekey", "prependedstring");

try {
    if (prependOp.get().booleanValue()) {
        System.out.printf("Prepend succeeded\n");
    }
    else {
        System.out.printf("Prepend failed\n");
    }
}
catch (Exception e) {
...
}

API Call	client.prepend(casunique, key, value, transcoder)
Asynchronous	yes
Description	Prepend a value to an existing key
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
long casunique	Unique value used to verify a key/value combination
String key	Document ID used to identify the value
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

The secondary form of the prepend() method supports the use of a custom transcoder for updating the key/value pair.

Check-and-Set Methods¶

The check-and-set methods provide a mechanism for updating information only if the client knows the check (CAS) value. This can be used to prevent clients from updating values in the database that may have changed since the client obtained the value. Methods for storing and updating information support a CAS method that allows you to ensure that the client is updating the version of the data that the client retrieved.

The check value is in the form of a 64-bit integer which is updated every time the value is modified, even if the update of the value does not modify the binary data. Attempting to set or update a key/value pair where the CAS value does not match the value stored on the server will fail.

The cas() methods are used to explicitly set the value only if the CAS supplied by the client matches the CAS on the server, analogous to the Set Operations method.

With all CAS operations, the CASResponse value returned indicates whether the operation succeeded or not, and if not why. The CASResponse is an Enum with three possible values:

• EXISTS

  The item exists, but the CAS value on the database does not match the value supplied to the CAS operation.

• NOT_FOUND

  The specified key does not exist in the database. An add() method should be used to add the key to the database.

• OK

  The CAS operation was successful and the updated value is stored in Couchbase

API Call	client.cas(key, casunique, value)
Asynchronous	no
Description	Compare and set a value providing the supplied CAS key matches
Returns	CASResponse ( Check and set object )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
Object value	Value to be stored

The first form of the cas() method allows for an item to be set in the database only if the CAS value supplied matches that stored on the server.

For example:

CASResponse casr = client.cas("caskey", casvalue, "new string value");

if (casr.equals(CASResponse.OK)) {
    System.out.println("Value was updated");
}
else if (casr.equals(CASResponse.NOT_FOUND)) {
    System.out.println("Value is not found");
}
else if (casr.equals(CASResponse.EXISTS)) {
    System.out.println("Value exists, but CAS didn't match");
}

API Call	client.cas(key, casunique, value, transcoder)
Asynchronous	no
Description	Compare and set a value providing the supplied CAS key matches
Returns	CASResponse ( Check and set object )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the method supports using a custom transcoder for storing a value.

API Call	client.cas(key, casunique, expiry, value, transcoder)
Asynchronous	no
Description	Compare and set a value providing the supplied CAS key matches
Returns	CASResponse ( Check and set object )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

This form of the cas() method updates both the key value and the expiry time for the value. For information on expiry values, see Expiry Values.

For example the following attempts to set the key caskey with an updated value, setting the expiry times to 3600 seconds (one hour).

Transcoder<Integer> tc = new IntegerTranscoder();
CASResponse casr = client.cas("caskey", casvalue, 3600, 1200, tc);

API Call	client.asyncCAS(key, casunique, value)
Asynchronous	yes
Description	Compare and set a value providing the supplied CAS key matches
Returns	Future<CASResponse> ( Asynchronous request value, as CASResponse )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
Object value	Value to be stored

Performs an asynchronous CAS operation on the given key/value. You can use this method to set a value using CAS without waiting for the response. The following example requests an update of a key, timing out after 5 seconds if the operation was not successful.

Future<CASResponse> future = client.asyncCAS("someKey", casvalue, "updatedvalue");

CASResponse casr;

try {
    casr = future.get(5, TimeUnit.SECONDS);
} catch(TimeoutException e) {
    future.cancel(false);
}

API Call	client.asyncCAS(key, casunique, value, transcoder)
Asynchronous	yes
Description	Compare and set a value providing the supplied CAS key matches
Returns	Future<CASResponse> ( Asynchronous request value, as CASResponse )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

Performs an asynchronous CAS operation on the given key/value using a custom transcoder. The example below shows the update of an existing value using a custom Integer transcoder.

Transcoder<Integer> tc = new IntegerTranscoder();
Future<CASResponse> future = client.asyncCAS("someKey", casvalue, 1200, tc);

CASResponse casr;

try {
    casr = future.get(5, TimeUnit.SECONDS);
} catch(TimeoutException e) {
    future.cancel(false);
}

API Call	client.asyncCAS(key, casunique, expiry, value, transcoder)
Asynchronous	yes
Description	Compare and set a value providing the supplied CAS key matches
Returns	Future<CASResponse> ( Asynchronous request value, as CASResponse )
Arguments
String key	Document ID used to identify the value
long casunique	Unique value used to verify a key/value combination
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

The final form of the asyncCAS() method supports a custom transcoder and setting the associated expiry value. For example, to update a value and set the expiry to 60 seconds:

Transcoder<Integer> tc = new IntegerTranscoder();
Future<CASResponse> future = client.asyncCAS("someKey", casvalue, 60, 1200, tc);

CASResponse casr;

try {
    casr = future.get(5, TimeUnit.SECONDS);
} catch(TimeoutException e) {
    future.cancel(false);
}

Delete Methods¶

The delete() method deletes an item in the database with the specified key. Delete operations are asynchronous only.

API Call	client.delete(key)
Asynchronous	yes
Description	Delete a key/value
Returns	OperationFuture<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value

For example, to delete an item you might use code similar to the following:

OperationFuture<Boolean> delOp =
    client.delete("samplekey");

try {
    if (delOp.get().booleanValue()) {
        System.out.printf("Delete succeeded\n");
    }
    else {
        System.out.printf("Delete failed\n");
    }

}
catch (Exception e) {
    System.out.println("Failed to delete " + e);
}

Decrement Methods¶

The decrement methods reduce the value of a given key if the corresponding value can be parsed to an integer value. These operations are provided at a protocol level to eliminate the need to get, update, and reset a simple integer value in the database. All the Java Client Library methods support the use of an explicit offset value that will be used to reduce the stored value in the database.

API Call	client.decr(key, offset)
Asynchronous	no
Description	Decrement the value of an existing numeric key. The Couchbase Server stores numbers as unsigned values. Therefore the lowest you can decrement is to zero.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)

The first form of the decr() method accepts the keyname and offset value to be used when reducing the server-side integer. For example, to decrement the server integer dlcounter by 5:

client.decr("dlcounter",5);

The return value is the updated value of the specified key.

API Call	client.decr(key, offset, default)
Asynchronous	no
Description	Decrement the value of an existing numeric key. The Couchbase Server stores numbers as unsigned values. Therefore the lowest you can decrement is to zero.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)
int default	Default value to increment/decrement if key does not exist

The second form of the decr() method will decrement the given key by the specified offset value if the key already exists, or set the key to the specified default value if the key does not exist. This can be used in situations where you are recording a counter value but do not know whether the key exists at the point of storage.

For example, if the key dlcounter does not exist, the following fragment will return 1000:

long newcount =
    client.decr("dlcount",1,1000);

System.out.printf("Updated counter is %d\n",newcount);

A subsequent identical call will return the value 999 as the key dlcount already exists.

API Call	client.decr(key, offset, default, expiry)
Asynchronous	no
Description	Decrement the value of an existing numeric key. The Couchbase Server stores numbers as unsigned values. Therefore the lowest you can decrement is to zero.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)
int default	Default value to increment/decrement if key does not exist
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).

The third form of the decr() method the decrement operation, with a default value and with the addition of setting an expiry time on the stored value. For example, to decrement a counter, using a default of 1000 if the value does not exist, and an expiry of 1 hour (3600 seconds):

long newcount =
    client.decr("dlcount",1,1000,3600);

For information on expiry values, see Expiry Values.

API Call	client.asyncDecr(key, offset)
Asynchronous	yes
Description	Decrement the value of an existing numeric key. The Couchbase Server stores numbers as unsigned values. Therefore the lowest you can decrement is to zero.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)

The asynchronous form of the asyncGet() method enables you to decrement a value without waiting for a response. This can be useful in situations where you do not need to know the updated value or merely want to perform a decrement and continue processing.

For example, to asynchronously decrement a given key:

OperationFuture<Long> decrOp =
    client.asyncDecr("samplekey",1,1000,24000);

Increment Methods¶

The increment methods enable you to increase a given stored integer value. These are the incremental equivalent of the decrement operations and work on the same basis; updating the value of a key if it can be parsed to an integer. The update operation occurs on the server and is provided at the protocol level. This simplifies what would otherwise be a two-stage get and set operation.

API Call	client.incr(key, offset)
Asynchronous	no
Description	Increment the value of an existing numeric key. Couchbase Server stores numbers as unsigned numbers, therefore if you try to increment an existing negative number, it will cause an integer overflow and return a non-logical numeric result. If a key does not exist, this method will initialize it with the zero or a specified value.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)

The first form of the incr() method accepts the keyname and offset (increment) value to be used when increasing the server-side integer. For example, to increment the server integer dlcounter by 5:

client.incr("dlcounter",5);

The return value is the updated value of the specified key.

API Call	client.incr(key, offset, default)
Asynchronous	no
Description	Increment the value of an existing numeric key. Couchbase Server stores numbers as unsigned numbers, therefore if you try to increment an existing negative number, it will cause an integer overflow and return a non-logical numeric result. If a key does not exist, this method will initialize it with the zero or a specified value.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)
int default	Default value to increment/decrement if key does not exist

The second form of the incr() method supports the use of a default value which will be used to set the corresponding key if that value does already exist in the database. If the key exists, the default value is ignored and the value is incremented with the provided offset value. This can be used in situations where you are recording a counter value but do not know whether the key exists at the point of storage.

For example, if the key dlcounter does not exist, the following fragment will return 1000:

long newcount =
    client.incr("dlcount",1,1000);

System.out.printf("Updated counter is %d\n",newcount);

A subsequent identical call will return the value 1001 as the key dlcount already exists and the value (1000) is incremented by 1.

API Call	client.incr(key, offset, default, expiry)
Asynchronous	no
Description	Increment the value of an existing numeric key. Couchbase Server stores numbers as unsigned numbers, therefore if you try to increment an existing negative number, it will cause an integer overflow and return a non-logical numeric result. If a key does not exist, this method will initialize it with the zero or a specified value.
Returns	long ( Numeric value )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)
int default	Default value to increment/decrement if key does not exist
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).

The third format of the incr() method supports setting an expiry value on the given key, in addition to a default value if key does not already exist.

For example, to increment a counter, using a default of 1000 if the value does not exist, and an expiry of 1 hour (3600 seconds):

long newcount =
    client.incr("dlcount",1,1000,3600);

For information on expiry values, see Expiry Values.

API Call	client.asyncIncr(key, offset)
Asynchronous	yes
Description	Increment the value of an existing numeric key. Couchbase Server stores numbers as unsigned numbers, therefore if you try to increment an existing negative number, it will cause an integer overflow and return a non-logical numeric result. If a key does not exist, this method will initialize it with the zero or a specified value.
Returns	Future<Long> ( Asynchronous request value, as Long )
Arguments
String key	Document ID used to identify the value
int offset	Integer offset value to increment/decrement (default 1)

The asyncIncr() method supports an asynchronous increment on the value for a corresponding key. Asynchronous increments are useful when you do not want to immediately wait for the return value of the increment operation.

OperationFuture<Long> incrOp =
    client.asyncIncr("samplekey",1,1000,24000);

Replace Methods¶

The replace() methods update an existing key/value pair in the database. If the specified key does not exist, then the operation will fail.

API Call	client.replace(key, expiry, value)
Asynchronous	yes
Description	Update an existing key with a new value
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored

The first form of the replace() method updates an existing value setting while supporting the explicit setting of the expiry time on the item. For example to update the samplekey :

OperationFuture<Boolean> replaceOp =
    client.replace("samplekey","updatedvalue",0);

The return value is a OperationFuture value with a Boolean base.

API Call	client.replace(key, expiry, value, transcoder)
Asynchronous	yes
Description	Update an existing key with a new value
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).
Object value	Value to be stored
Transcoder transcoder	Transcoder class to be used to serialize value

The second form of the replace() method is identical o the first, but also supports using a custom Transcoder in place of the default transcoder.

Touch Methods¶

The touch() methods allow you to update the expiration time on a given key. This can be useful for situations where you want to prevent an item from expiring without resetting the associated value. For example, for a session database you might want to keep the session alive in the database each time the user accesses a web page without explicitly updating the session value, keeping the user’s session active and available.

API Call	client.touch(key, expiry)
Asynchronous	yes
Description	Update the expiry time of an item
Returns	Future<Boolean> ( Asynchronous request value, as Boolean )
Arguments
String key	Document ID used to identify the value
int expiry	Expiry time for key. Values larger than 30*24*60*60 seconds (30 days) are interpreted as absolute times (from the epoch).

The first form of the touch() provides a simple key/expiry call to update the expiry time on a given key. For example, to update the expiry time on a session for another 5 minutes:

OperationFuture<Boolean> touchOp =
    client.touch("sessionid",300);

Statistics Operations¶

The Couchbase Java Client Library includes support for obtaining statistic information from all of the servers defined within a CouchbaseClient object. A summary of the commands is provided below.

API Call	client.getStats()
Asynchronous	no
Description	Get the database statistics
Returns	Object ( Binary object )
Arguments
	None

The first form of the getStats() command gets the statistics from all of the servers configured in your CouchbaseClient object. The information is returned in the form of a nested Map, first containing the address of configured server, and then within each server the individual statistics for that server.

API Call	client.getStats(statname)
Asynchronous	no
Description	Get the database statistics
Returns	Object ( Binary object )
Arguments
String statname	Group name of a statistic for selecting individual statistic value

The second form of the getStats() command gets the specified group of statistics from all of the servers configured in your CouchbaseClient object. The information is returned in the form of a nested Map, first containing the address of configured server, and then within each server the individual statistics for that server.

Java Troubleshooting¶

This Couchbase SDK Java provides a complete interface to Couchbase Server through the Java programming language. For more on Couchbase Server and Java read our Java SDK Getting Started Guide followed by our in-depth Couchbase and Java tutorial. We recommended Java SE 6 (or higher) for running the Couchbase Client Library.

This section covers the following topics:

• Logging from the Java SDK

• Handling Timeouts

• Bulk Load and Exponential Backoff

• Retrying After Receiving a Temporary Failure

Configuring Logging¶

Occasionally when you are troubleshooting an issue with a clustered deployment, you may find it helpful to use additional information from the Couchbase Java SDK logging. The SDK uses JDK logging and this can be configured by specifying a runtime define and adding some additional logging properties. There are two ways to set up Java SDK logging:

• Use spymemcached to log from the Java SDK. Since the SDK uses spymemcached and is compatible with spymemcached, you can use the logging provided to output SDK-level information.

• Set your JDK properties to log Couchbase Java SDK information.

• Provide logging from your application.

To provide logging via spymemcached:

System.setProperty("net.spy.log.LoggerImpl", "net.spy.memcached.compat.log.SunLogger");

or

System.setProperty("net.spy.log.LoggerImpl", "net.spy.memcached.compat.log.Log4JLogger");

The default logger simply logs everything to the standard error stream. To provide logging via the JDK, if you are running a command-line Java program, you can run the program with logging by setting a property:

-Djava.util.logging.config.file=logging.properties

The other alternative is create a logging.properties and add it to your in your classpath:

logging.properties
handlers = java.util.logging.ConsoleHandler
java.util.logging.ConsoleHandler.level = ALL
java.util.logging.ConsoleHandler.formatter = java.util.logging.SimpleFormatter
com.couchbase.client.vbucket.level = FINEST
com.couchbase.client.vbucket.config.level = FINEST
com.couchbase.client.level = FINEST

The final option is to provide logging from your actual Java application. If you are writing your application in an IDE which manages command-line operations for you, it may be easier if you express logging in your application code. Here is an example:

// Tell things using spymemcached logging to use internal SunLogger API
        Properties systemProperties = System.getProperties();
        systemProperties.put("net.spy.log.LoggerImpl", "net.spy.memcached.compat.log.SunLogger");
        System.setProperties(systemProperties);

        Logger.getLogger("net.spy.memcached").setLevel(Level.FINEST);
        Logger.getLogger("com.couchbase.client").setLevel(Level.FINEST);
        Logger.getLogger("com.couchbase.client.vbucket").setLevel(Level.FINEST);

        //get the top Logger
        Logger topLogger = java.util.logging.Logger.getLogger("");

        // Handler for console (reuse it if it already exists)
        Handler consoleHandler = null;
        //see if there is already a console handler
        for (Handler handler : topLogger.getHandlers()) {
            if (handler instanceof ConsoleHandler) {
                //found the console handler
                consoleHandler = handler;
                break;
            }
        }

        if (consoleHandler == null) {
            //there was no console handler found, create a new one
            consoleHandler = new ConsoleHandler();
            topLogger.addHandler(consoleHandler);
        }

        //set the console handler to fine:
        consoleHandler.setLevel(java.util.logging.Level.FINEST);

Handling Timeouts¶

The Java client library has a set of synchronous and asynchronous methods. While it does not happen in most situations, occasionally network IO can become congested, nodes can fail, or memory pressure can lead to situations where an operation can timeout.

When a timeout occurs, most of the synchronous methods on the client will return a RuntimeException showing a timeout as the root cause. Since the asynchronous operations give more specific control over how long it takes for an operation to be successful or unsuccessful, asynchronous operations throw a checked TimeoutException.

As an application developer, it is best to think about what you would do after this timeout. This may be something such as showing the user a message, it may be doing nothing, or it may be going to some other system for additional data.

In some cases you might want to retry the operation, but you should consider this carefully before performing the retry in your code; sometimes a retry may exacerbate the underlying problem that caused the timeout. If you choose to do a retry, providing in the form of a backoff or exponential backoff is advisable. This can be thought of as a pressure relief valve for intermittent resource problems. For more information on backoff and exponential backoff, see Bulk Load and Exponential Backoff.

Timing-out and Blocking¶

If your application creates a large number of asynchronous operations, you may also encounter timeouts immediately in response to the requests. When you perform an asynchronous operation, Couchbase Java SDK creates an object and puts the object into a request queue. The object and the request are stored in Java runtime memory, in other words, they are stored in local to your Java application runtime memory and require some amount of Java Virtual Machine IO to be serviced.

Rather than write so many asynchronous operations that can overwhelm a JVM and generate out of memory errors for the JVM, you can rely on SDK-level timeouts. The default behavior of the Java SDK is to start to immediately timeout asynchronous operations if the queue of operations to be sent to the server is overwhelmed.

You can also choose to control the volume of asynchronous requests that are issued by your application by setting a timeout for blocking. You might want to do this for a bulk load of data so that you do not overwhelm your JVM. The following is an example:

List<URI> baselist = new ArrayList<URI>();
        baselist.add(new URI("http://localhost:8091/pools"));

        CouchbaseConnectionFactoryBuilder cfb = new CouchbaseConnectionFactoryBuilder();
        cfb.setOpQueueMaxBlockTime(5000); // wait up to 5 seconds when trying to enqueue an operation

        CouchbaseClient myclient = new CouchbaseClient(cfb.buildCouchbaseConnection(baselist, "default", "default", ""));

Bulk Load and Exponential Backoff¶

When you bulk load data to Couchbase Server, you can accidentally overwhelm available memory in the Couchbase cluster before it can store data on disk. If this happens, Couchbase Server will immediately send a response indicating the operation cannot be handled at the moment but can be handled later.

This is sometimes referred to as “handling Temp OOM”, where where OOM means out of memory. Note though that the actual temporary failure could be sent back for reasons other than OOM. However, temporary OOM is the most common underlying cause for this error.

To handle this problem, you could perform an exponential backoff as part of your bulk load. The backoff essentially reduces the number of requests sent to Couchbase Server as it receives OOM errors:

package com.couchbase.sample.dataloader;

import com.couchbase.client.CouchbaseClient;
import java.io.IOException;
import java.net.URI;
import java.util.List;
import net.spy.memcached.internal.OperationFuture;
import net.spy.memcached.ops.OperationStatus;

/**
 *
   * The StoreHandler exists mainly to abstract the need to store things
   * to the Couchbase Cluster even in environments where we may receive
   * temporary failures.
 *
 * @author ingenthr
 */
public class StoreHandler {

  CouchbaseClient cbc;
  private final List<URI> baselist;
  private final String bucketname;
  private final String password;

  /**
   *
   * Create a new StoreHandler.  This will not be ready until it's initialized
   * with the init() call.
   *
   * @param baselist
   * @param bucketname
   * @param password
   */
  public StoreHandler(List<URI> baselist, String bucketname, String password) {
    this.baselist = baselist; // TODO: maybe copy this?
    this.bucketname = bucketname;
    this.password = password;


  }

  /**
   * Initialize this StoreHandler.
   *
   * This will build the connections for the StoreHandler and prepare it
   * for use.  Initialization is separated from creation to ensure we would
   * not throw exceptions from the constructor.
   *
   *
   * @return StoreHandler
   * @throws IOException
   */
  public StoreHandler init() throws IOException {
    // I prefer to avoid exceptions from constructors, a legacy we're kind
    // of stuck with, so wrapped here
    cbc = new CouchbaseClient(baselist, bucketname, password);
    return this;
  }

  /**
   *
   * Perform a regular, asynchronous set.
   *
   * @param key
   * @param exp
   * @param value
   * @return the OperationFuture<Boolean> that wraps this set operation
   */
  public OperationFuture<Boolean> set(String key, int exp, Object value) {
    return cbc.set(key, exp, cbc);
  }

  /**
   * Continuously try a set with exponential backoff until number of tries or
   * successful.  The exponential backoff will wait a maximum of 1 second, or
   * whatever
   *
   * @param key
   * @param exp
   * @param value
   * @param tries number of tries before giving up
   * @return the OperationFuture<Boolean> that wraps this set operation
   */
  public OperationFuture<Boolean> contSet(String key, int exp, Object value,
          int tries) {
    OperationFuture<Boolean> result = null;
    OperationStatus status;
    int backoffexp = 0;

    try {
      do {
        if (backoffexp > tries) {
          throw new RuntimeException("Could not perform a set after "
                  + tries + " tries.");
        }
        result = cbc.set(key, exp, value);
        status = result.getStatus(); // blocking call, improve if needed
        if (status.isSuccess()) {
          break;
        }
        if (backoffexp > 0) {
          double backoffMillis = Math.pow(2, backoffexp);
          backoffMillis = Math.min(1000, backoffMillis); // 1 sec max
          Thread.sleep((int) backoffMillis);
          System.err.println("Backing off, tries so far: " + backoffexp);
        }
        backoffexp++;

        if (!status.isSuccess()) {
          System.err.println("Failed with status: " + status.getMessage());
        }

      } while (status.getMessage().equals("Temporary failure"));
    } catch (InterruptedException ex) {
      System.err.println("Interrupted while trying to set.  Exception:"
              + ex.getMessage());
    }

    if (result == null) {
      throw new RuntimeException("Could not carry out operation."); // rare
    }

    // note that other failure cases fall through.  status.isSuccess() can be
    // checked for success or failure or the message can be retrieved.
    return result;
  }
}

There is also a setting you can provide at the connection-level for Couchbase Java SDK that will also help you avoid too many asynchronous requests:

List<URI> baselist = new ArrayList<URI>();
        baselist.add(new URI("http://localhost:8091/pools"));

        CouchbaseConnectionFactoryBuilder cfb = new CouchbaseConnectionFactoryBuilder();
        cfb.setOpTimeout(10000);  // wait up to 10 seconds for an operation to succeed
        cfb.setOpQueueMaxBlockTime(5000); // wait up to 5 seconds when trying to enqueue an operation

        CouchbaseClient myclient = new CouchbaseClient(cfb.buildCouchbaseConnection(baselist, "default", "default", ""));

Retrying After Receiving a Temporary Failure¶

If you send too many requests all at once to Couchbase, you can create a out of memory problem, and the server will send back a temporary failure message. The message indicates you can retry the operation, however the server will not slow down significantly; it just does not handle the request. In contrast, other database systems will become slower for all operations under load.

This gives your application a bit more control since the temporary failure messages gives you the opportunity to provide a backoff mechanism and retry operations in your application logic.

Java Virtual Machine Tuning Guidelines¶

Generally speaking, there is no reason to adjust any Java Virtual Machine parameters when using the Couchbase Java Client. In fact, in general you should not start with specific tuning, but instead should use defaults from the application server first, then measure application metrics such as throughput and response time. Then, if there is a need to make an improvement, make adjustments and re-measure.

The recommendations here are based on the Oracle (formerly Sun) HotSpot Virtual Machine and derivations such as the Java Virtual Machine shipped with Mac OS X and the OpenJDK project. Other Java virtual machines likely behave similarly.

It should be noted that by default, garbage collection times may easily go over 1sec. This can lead to higher than expected response times or even timeouts, as the default timeout is 2.5 seconds. This is true with simple tests even on systems with lots of CPUs and a good amount of memory.

The reason for this is that for the most part, by default, the JVM is weighted toward throughput instead of latency. Of course, much of this can be controlled with GC tuning on the JVM. With the hotspot JVM, look to this whitepaper: http://www.oracle.com/technetwork/java/javase/memorymanagement-whitepaper-150215.pdf

In the referenced whitepaper, the Concurrent Mark Sweep collector is recommended if your applciation needs short pauses. It also recommends advising the JVM to try to shorten pause times. Given the Couchbase client’s 2.5 second default timeout, with our basic testing we found the following to be useful:

-XX:+UseConcMarkSweepGC -XX:MaxGCPauseMillis=850

The whitepaper refers to a couple of tools which may be useful in gathering information on JVM GC performance. For example, adding -XX:+PrintGCDetails and -XX:+PrintGCTimeStamps are a simple way to generate log messages which you may correlate to application behavior. The logs may show a full GC event taking, perhaps, several seconds during which no processing occurs and operations may timeout. Adjusting parameters related to how to perform a full GC, which collector to use, how long to pause the VM during GC and even adding incremental mode may help, depending on your application’s workload. One other common tool for getting information is JConsole (http://docs.oracle.com/javase/6/docs/technotes/guides/management/jconsole.html). JConsole is more of an interactive tool, but it may help you identify changes you may want to make in the different memory spaces used by the JVM to further reduce the need to run a GC on the old generation.

There is a CPU time tradeoff when setting these tuning parameters. There are also other parameters which may provide additional help referenced in the whitepaper.

If you happen to be using JDK 7 update 4 or later, the G1 collector may be an even better option. Again, you should be guided by measuring performance from the application level.

Even with these, our testing showed some GCs near a half a second. While the Couchbase Client allows tuning of the timeout time to drop as low as you wish, we do not recommend dropping it much below one second unless you are planning to tune other parts of the system beyond the JVM.

For example, most people run applications on networks that do not offer any guarantee around response time. If the network is oversubscribed or minor blips occur on the network, there can be TCP retransmissions. While many TCP implementations may ignore it, RFC 2988 specifies rounding up to 1sec when calculating TCP retransmit timeouts.

Achieving either maximum throughput or minimum per-operation latency can be enhanced with JVM tuning, supported by overall system tuning at the extremes.

Appendix: Release Notes¶

The following sections provide release notes for individual release versions of Couchbase Client Library Java. To browse or submit new issues, see Couchbase Client Library Java Issues Tracker.

Release Notes for Couchbase Client Library Java 1.0.3 GA (30 July 2012)¶

Fixes in 1.0.3

• It was found that in some circumstances, the client can fail to update to the changed cluster topology if there was a failure and either the instance wide client timeout or the operations the client is doing have a short (i.e., less than 700ms or so) timeout. JCBC-88.

  Issues : JCBC-88, JCBC-88

• It was found that in the dependent spymemcached client library that errors encountered in optimized set operations would not be handled correctly and thus application code would receive unexpected errors during a rebalance. This has been worked around in this release by disabling optimization. This may have a negilgable drop in throughput but shorter latencies.

• If using the CouchbaseConnectionFactoryBuilder, authentication could be ignored by the client library.

  Issues : JCBC-53

• Ensure the configuration is updated even if the node the client is intended to receive updates from fails without closing the TCP connection. Make sure these configuration checks are reliable and do not consume significant resources.

  Issues : JCBC-54

Known Issues in 1.0.3

• As a workaround to a reliability under rebalance issue, optimization has been disabled in this release. This can cause a negligible drop in throughput but have better per-operation latency.

  Issues : JCBC-89

Release Notes for Couchbase Client Library Java 1.0.2 GA (5 April 2012)¶

Fixes in 1.0.2

• An issue which affects memcached bucket types, where it was found that the hashing was not compatible with Couchbase Server’s proxy port (a.k.a. moxi) has been fixed in this release. It is also incompatible with the spymemcached 2.7.x compatibility with Couchbase (and Membase). Note that this means the use of the 1.0.2 client is INCOMPATIBLE with 1.0.1 and 1.0.0.

  Issues : JCBC-29

• An issue which would prevent failover in some situations was fixed in this release. Prior to this fix, a permanent failure of the node the client was receiving configurations from (typically from the first node in the list) would cause the client to stick with an old configuration, and thus it would not know about any failovers or changes to cluster topology.

  Issues : JCBC-19

Release Notes for Couchbase Client Library Java 1.0.1 GA (25 January 2012)¶

Fixes in 1.0.1

• Some Maven issues with the client libraries were fixed.

• A major bug in 1.0.0 causing incorrect hashing of vBuckets was fixed and addressed in 1.0.1

Release Notes for Couchbase Client Library Java 1.0.0 GA (23 January 2012)¶

New Features and Behavior Changes in 1.0.0

• The spymemcached library functionality is now avaliable via Couchbase-client and spymemcached libraries. Couchbase Connections, Connection Factory and the storage and retrieval operations is abstracted in the Couchbase-client library and ought to be the predominant library to be used by Java programs. Memcached functionality is still available with spymemcached.

  Consequently, the package structure has a new com.couchbase.client package in addition to the exisiting net.spy.memcached package.

  For example, the connection to Couchbase can be obtained using the Couchbase-client library objects and methods.

  List<URI> uris = new LinkedList<URI>();
  
    // Connect to localhost or to the appropriate URI
    uris.add(URI.create("http://127.0.0.1:8091/pools&quot;));
    try {
    client = new CouchbaseClient(uris, "default", "");
    } catch (Exception e) {
    System.err.println("Error connecting to Couchbase: "
  
  e.getMessage());
  System.exit(0);
  }
  

or using the CouchbaseConnectionFactory as below.

CouchbaseConnectionFactory cf = new CouchbaseConnectionFactory(uris,
   "rags", "password");
   client = new CouchbaseClient((CouchbaseConnectionFactory) cf);